Probabilistic Planning via Heuristic Forward Search and Weighted Model Counting

We present a new algorithm for probabilistic planning with no observability. Our algorithm, called Probabilistic-FF, extends the heuristic forward-search machinery of Conformant-FF to problems with probabilistic uncertainty about both the initial state and action effects. Specifically, Probabilistic-FF combines Conformant-FFs techniques with a powerful machinery for weighted model counting in (weighted) CNFs, serving to elegantly define both the search space and the heuristic function. Our evaluation of Probabilistic-FF shows its fine scalability in a range of probabilistic domains, constituting a several orders of magnitude improvement over previous results in this area. We use a problematic case to point out the main open issue to be addressed by further research.

On Graphical Modeling of Preference and Importance

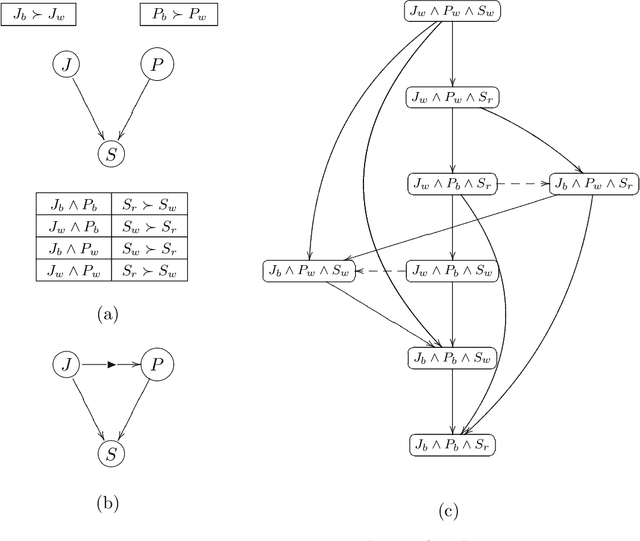
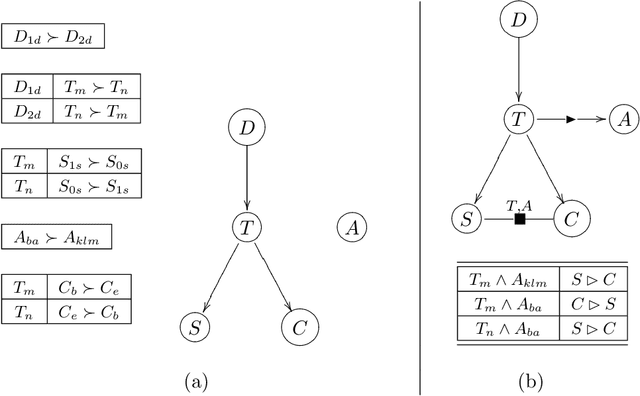
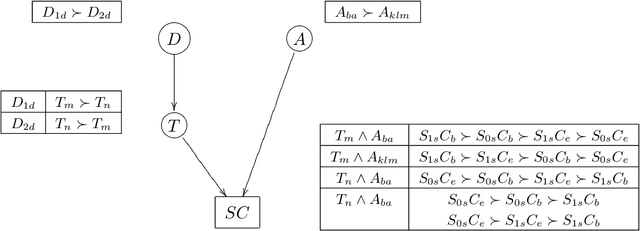
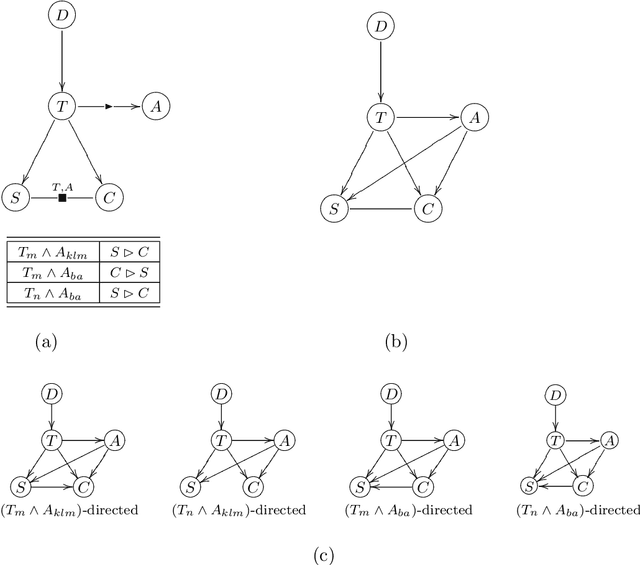
In recent years, CP-nets have emerged as a useful tool for supporting preference elicitation, reasoning, and representation. CP-nets capture and support reasoning with qualitative conditional preference statements, statements that are relatively natural for users to express. In this paper, we extend the CP-nets formalism to handle another class of very natural qualitative statements one often uses in expressing preferences in daily life - statements of relative importance of attributes. The resulting formalism, TCP-nets, maintains the spirit of CP-nets, in that it remains focused on using only simple and natural preference statements, uses the ceteris paribus semantics, and utilizes a graphical representation of this information to reason about its consistency and to perform, possibly constrained, optimization using it. The extra expressiveness it provides allows us to better model tradeoffs users would like to make, more faithfully representing their preferences.

CP-nets: A Tool for Representing and Reasoning withConditional Ceteris Paribus Preference Statements

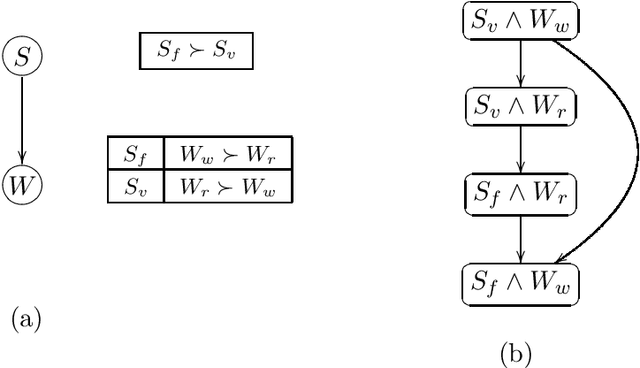
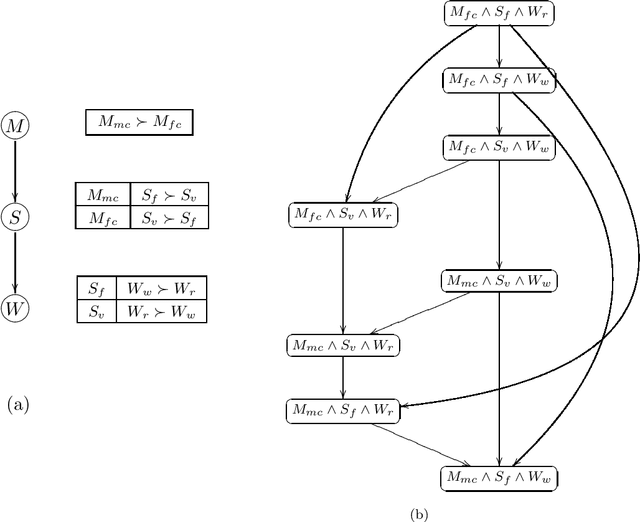
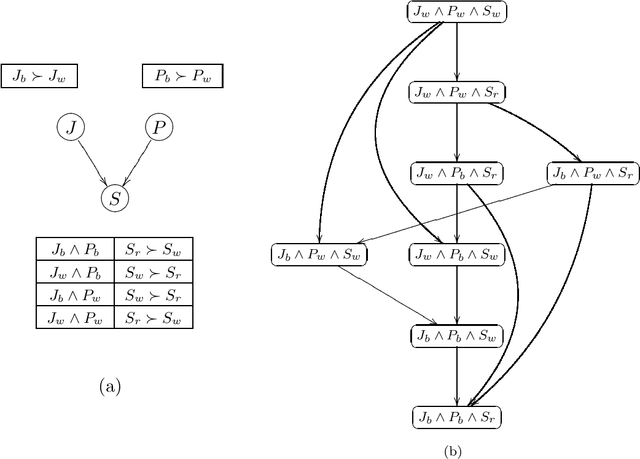
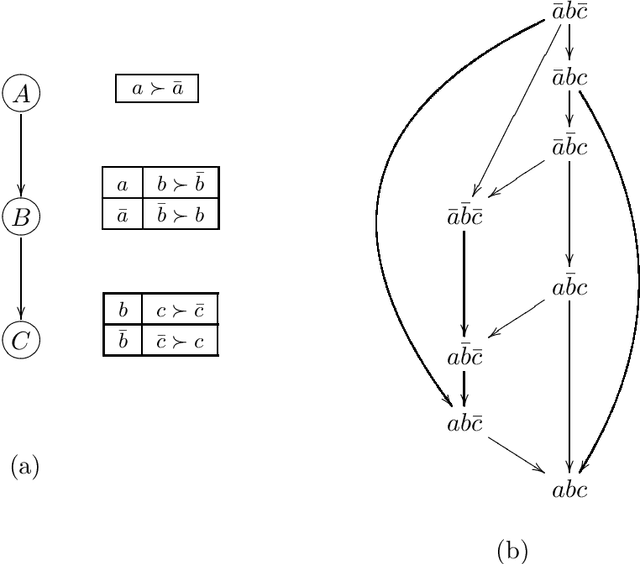
Information about user preferences plays a key role in automated decision making. In many domains it is desirable to assess such preferences in a qualitative rather than quantitative way. In this paper, we propose a qualitative graphical representation of preferences that reflects conditional dependence and independence of preference statements under a ceteris paribus (all else being equal) interpretation. Such a representation is often compact and arguably quite natural in many circumstances. We provide a formal semantics for this model, and describe how the structure of the network can be exploited in several inference tasks, such as determining whether one outcome dominates (is preferred to) another, ordering a set outcomes according to the preference relation, and constructing the best outcome subject to available evidence.

Structure and Complexity in Planning with Unary Operators

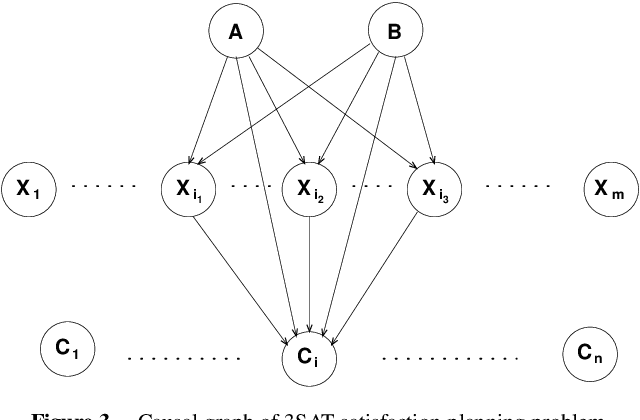
Unary operator domains -- i.e., domains in which operators have a single effect -- arise naturally in many control problems. In its most general form, the problem of STRIPS planning in unary operator domains is known to be as hard as the general STRIPS planning problem -- both are PSPACE-complete. However, unary operator domains induce a natural structure, called the domain's causal graph. This graph relates between the preconditions and effect of each domain operator. Causal graphs were exploited by Williams and Nayak in order to analyze plan generation for one of the controllers in NASA's Deep-Space One spacecraft. There, they utilized the fact that when this graph is acyclic, a serialization ordering over any subgoal can be obtained quickly. In this paper we conduct a comprehensive study of the relationship between the structure of a domain's causal graph and the complexity of planning in this domain. On the positive side, we show that a non-trivial polynomial time plan generation algorithm exists for domains whose causal graph induces a polytree with a constant bound on its node indegree. On the negative side, we show that even plan existence is hard when the graph is a directed-path singly connected DAG. More generally, we show that the number of paths in the causal graph is closely related to the complexity of planning in the associated domain. Finally we relate our results to the question of complexity of planning with serializable subgoals.