Probabilistic Planning via Heuristic Forward Search and Weighted Model Counting

We present a new algorithm for probabilistic planning with no observability. Our algorithm, called Probabilistic-FF, extends the heuristic forward-search machinery of Conformant-FF to problems with probabilistic uncertainty about both the initial state and action effects. Specifically, Probabilistic-FF combines Conformant-FFs techniques with a powerful machinery for weighted model counting in (weighted) CNFs, serving to elegantly define both the search space and the heuristic function. Our evaluation of Probabilistic-FF shows its fine scalability in a range of probabilistic domains, constituting a several orders of magnitude improvement over previous results in this area. We use a problematic case to point out the main open issue to be addressed by further research.

Engineering Benchmarks for Planning: the Domains Used in the Deterministic Part of IPC-4

In a field of research about general reasoning mechanisms, it is essential to have appropriate benchmarks. Ideally, the benchmarks should reflect possible applications of the developed technology. In AI Planning, researchers more and more tend to draw their testing examples from the benchmark collections used in the International Planning Competition (IPC). In the organization of (the deterministic part of) the fourth IPC, IPC-4, the authors therefore invested significant effort to create a useful set of benchmarks. They come from five different (potential) real-world applications of planning: airport ground traffic control, oil derivative transportation in pipeline networks, model-checking safety properties, power supply restoration, and UMTS call setup. Adapting and preparing such an application for use as a benchmark in the IPC involves, at the time, inevitable (often drastic) simplifications, as well as careful choice between, and engineering of, domain encodings. For the first time in the IPC, we used compilations to formulate complex domain features in simple languages such as STRIPS, rather than just dropping the more interesting problem constraints in the simpler language subsets. The article explains and discusses the five application domains and their adaptation to form the PDDL test suites used in IPC-4. We summarize known theoretical results on structural properties of the domains, regarding their computational complexity and provable properties of their topology under the h+ function (an idealized version of the relaxed plan heuristic). We present new (empirical) results illuminating properties such as the quality of the most wide-spread heuristic functions (planning graph, serial planning graph, and relaxed plan), the growth of propositional representations over instance size, and the number of actions available to achieve each fact; we discuss these data in conjunction with the best results achieved by the different kinds of planners participating in IPC-4.

Where 'Ignoring Delete Lists' Works: Local Search Topology in Planning Benchmarks

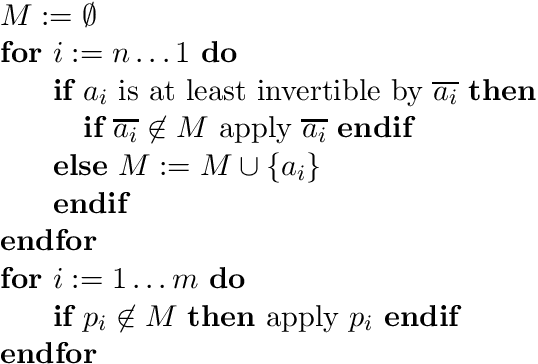
Between 1998 and 2004, the planning community has seen vast progress in terms of the sizes of benchmark examples that domain-independent planners can tackle successfully. The key technique behind this progress is the use of heuristic functions based on relaxing the planning task at hand, where the relaxation is to assume that all delete lists are empty. The unprecedented success of such methods, in many commonly used benchmark examples, calls for an understanding of what classes of domains these methods are well suited for. In the investigation at hand, we derive a formal background to such an understanding. We perform a case study covering a range of 30 commonly used STRIPS and ADL benchmark domains, including all examples used in the first four international planning competitions. We *prove* connections between domain structure and local search topology -- heuristic cost surface properties -- under an idealized version of the heuristic functions used in modern planners. The idealized heuristic function is called h^+, and differs from the practically used functions in that it returns the length of an *optimal* relaxed plan, which is NP-hard to compute. We identify several key characteristics of the topology under h^+, concerning the existence/non-existence of unrecognized dead ends, as well as the existence/non-existence of constant upper bounds on the difficulty of escaping local minima and benches. These distinctions divide the (set of all) planning domains into a taxonomy of classes of varying h^+ topology. As it turns out, many of the 30 investigated domains lie in classes with a relatively easy topology. Most particularly, 12 of the domains lie in classes where FFs search algorithm, provided with h^+, is a polynomial solving mechanism. We also present results relating h^+ to its approximation as implemented in FF. The behavior regarding dead ends is provably the same. We summarize the results of an empirical investigation showing that, in many domains, the topological qualities of h^+ are largely inherited by the approximation. The overall investigation gives a rare example of a successful analysis of the connections between typical-case problem structure, and search performance. The theoretical investigation also gives hints on how the topological phenomena might be automatically recognizable by domain analysis techniques. We outline some preliminary steps we made into that direction.

The Deterministic Part of IPC-4: An Overview

We provide an overview of the organization and results of the deterministic part of the 4th International Planning Competition, i.e., of the part concerned with evaluating systems doing deterministic planning. IPC-4 attracted even more competing systems than its already large predecessors, and the competition event was revised in several important respects. After giving an introduction to the IPC, we briefly explain the main differences between the deterministic part of IPC-4 and its predecessors. We then introduce formally the language used, called PDDL2.2 that extends PDDL2.1 by derived predicates and timed initial literals. We list the competing systems and overview the results of the competition. The entire set of data is far too large to be presented in full. We provide a detailed summary; the complete data is available in an online appendix. We explain how we awarded the competition prizes.

Ordered Landmarks in Planning

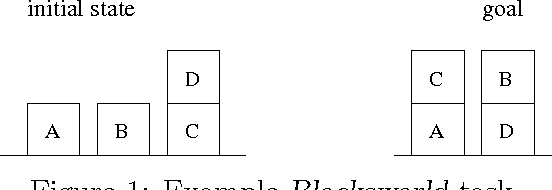
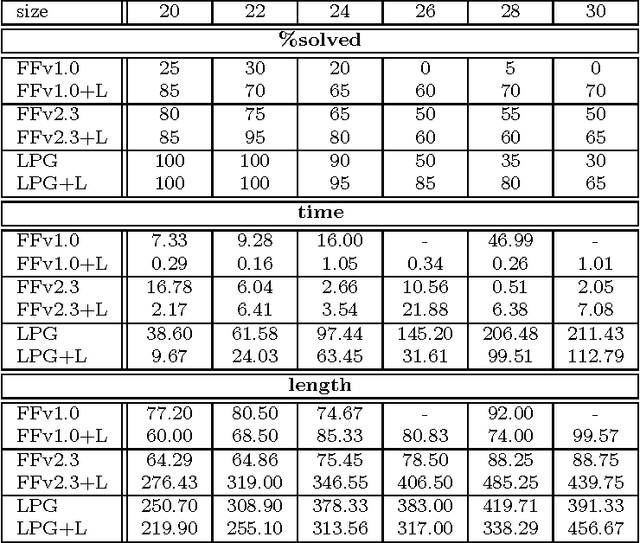
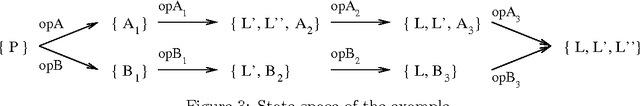
Many known planning tasks have inherent constraints concerning the best order in which to achieve the goals. A number of research efforts have been made to detect such constraints and to use them for guiding search, in the hope of speeding up the planning process. We go beyond the previous approaches by considering ordering constraints not only over the (top-level) goals, but also over the sub-goals that will necessarily arise during planning. Landmarks are facts that must be true at some point in every valid solution plan. We extend Koehler and Hoffmann's definition of reasonable orders between top level goals to the more general case of landmarks. We show how landmarks can be found, how their reasonable orders can be approximated, and how this information can be used to decompose a given planning task into several smaller sub-tasks. Our methodology is completely domain- and planner-independent. The implementation demonstrates that the approach can yield significant runtime performance improvements when used as a control loop around state-of-the-art sub-optimal planning systems, as exemplified by FF and LPG.

The Metric-FF Planning System: Translating "Ignoring Delete Lists" to Numeric State Variables

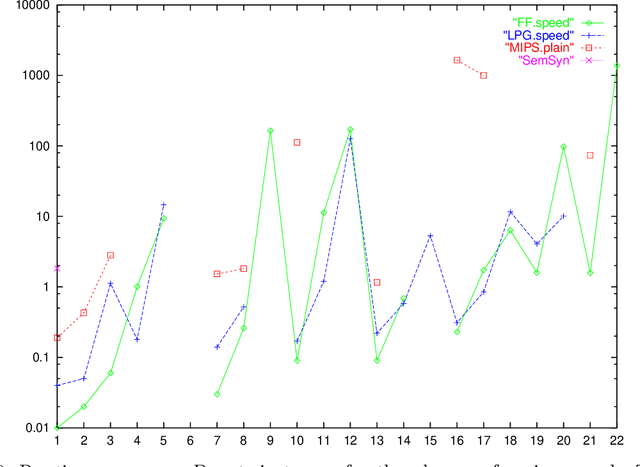
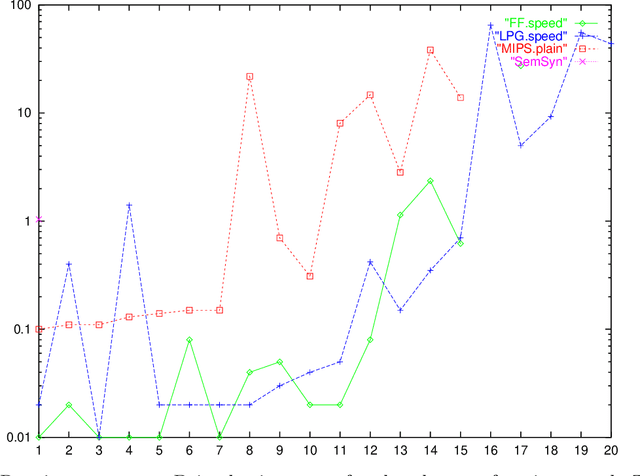
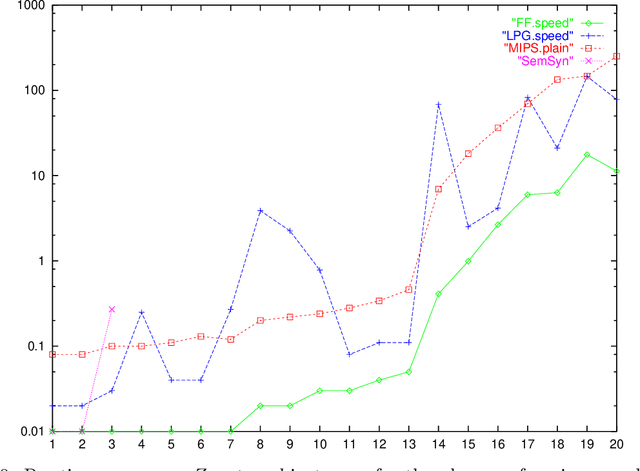
Planning with numeric state variables has been a challenge for many years, and was a part of the 3rd International Planning Competition (IPC-3). Currently one of the most popular and successful algorithmic techniques in STRIPS planning is to guide search by a heuristic function, where the heuristic is based on relaxing the planning task by ignoring the delete lists of the available actions. We present a natural extension of ``ignoring delete lists'' to numeric state variables, preserving the relevant theoretical properties of the STRIPS relaxation under the condition that the numeric task at hand is ``monotonic''. We then identify a subset of the numeric IPC-3 competition language, ``linear tasks'', where monotonicity can be achieved by pre-processing. Based on that, we extend the algorithms used in the heuristic planning system FF to linear tasks. The resulting system Metric-FF is, according to the IPC-3 results which we discuss, one of the two currently most efficient numeric planners.

The FF Planning System: Fast Plan Generation Through Heuristic Search

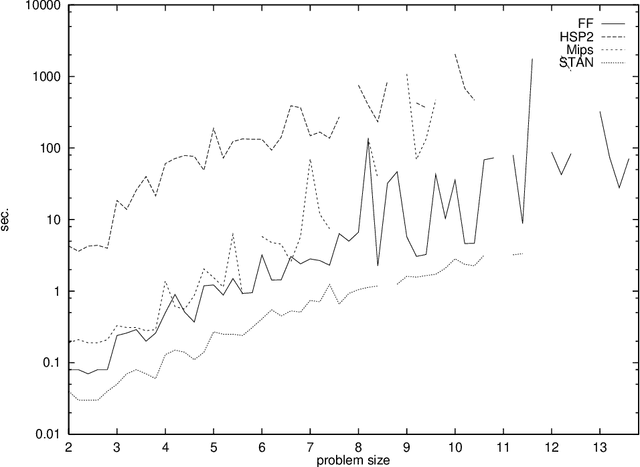
We describe and evaluate the algorithmic techniques that are used in the FF planning system. Like the HSP system, FF relies on forward state space search, using a heuristic that estimates goal distances by ignoring delete lists. Unlike HSP's heuristic, our method does not assume facts to be independent. We introduce a novel search strategy that combines hill-climbing with systematic search, and we show how other powerful heuristic information can be extracted and used to prune the search space. FF was the most successful automatic planner at the recent AIPS-2000 planning competition. We review the results of the competition, give data for other benchmark domains, and investigate the reasons for the runtime performance of FF compared to HSP.

On Reasonable and Forced Goal Orderings and their Use in an Agenda-Driven Planning Algorithm

The paper addresses the problem of computing goal orderings, which is one of the longstanding issues in AI planning. It makes two new contributions. First, it formally defines and discusses two different goal orderings, which are called the reasonable and the forced ordering. Both orderings are defined for simple STRIPS operators as well as for more complex ADL operators supporting negation and conditional effects. The complexity of these orderings is investigated and their practical relevance is discussed. Secondly, two different methods to compute reasonable goal orderings are developed. One of them is based on planning graphs, while the other investigates the set of actions directly. Finally, it is shown how the ordering relations, which have been derived for a given set of goals G, can be used to compute a so-called goal agenda that divides G into an ordered set of subgoals. Any planner can then, in principle, use the goal agenda to plan for increasing sets of subgoals. This can lead to an exponential complexity reduction, as the solution to a complex planning problem is found by solving easier subproblems. Since only a polynomial overhead is caused by the goal agenda computation, a potential exists to dramatically speed up planning algorithms as we demonstrate in the empirical evaluation, where we use this method in the IPP planner.