Edge-Based Graph Component Pooling

Graph-structured data naturally occurs in many research fields, such as chemistry and sociology. The relational information contained therein can be leveraged to statistically model graph properties through geometrical deep learning. Graph neural networks employ techniques, such as message-passing layers, to propagate local features through a graph. However, message-passing layers can be computationally expensive when dealing with large and sparse graphs. Graph pooling operators offer the possibility of removing or merging nodes in such graphs, thus lowering computational costs. However, pooling operators that remove nodes cause data loss, and pooling operators that merge nodes are often computationally expensive. We propose a pooling operator that merges nodes so as not to cause data loss but is also conceptually simple and computationally inexpensive. We empirically demonstrate that the proposed pooling operator performs statistically significantly better than edge pool on four popular benchmark datasets while reducing time complexity and the number of trainable parameters by 70.6% on average. Compared to another maximally powerful method named Graph Isomporhic Network, we show that we outperform them on two popular benchmark datasets while reducing the number of learnable parameters on average by 60.9%.

Dynamic Local Search for the Maximum Clique Problem

In this paper, we introduce DLS-MC, a new stochastic local search algorithm for the maximum clique problem. DLS-MC alternates between phases of iterative improvement, during which suitable vertices are added to the current clique, and plateau search, during which vertices of the current clique are swapped with vertices not contained in the current clique. The selection of vertices is solely based on vertex penalties that are dynamically adjusted during the search, and a perturbation mechanism is used to overcome search stagnation. The behaviour of DLS-MC is controlled by a single parameter, penalty delay, which controls the frequency at which vertex penalties are reduced. We show empirically that DLS-MC achieves substantial performance improvements over state-of-the-art algorithms for the maximum clique problem over a large range of the commonly used DIMACS benchmark instances.

CP-nets: A Tool for Representing and Reasoning withConditional Ceteris Paribus Preference Statements

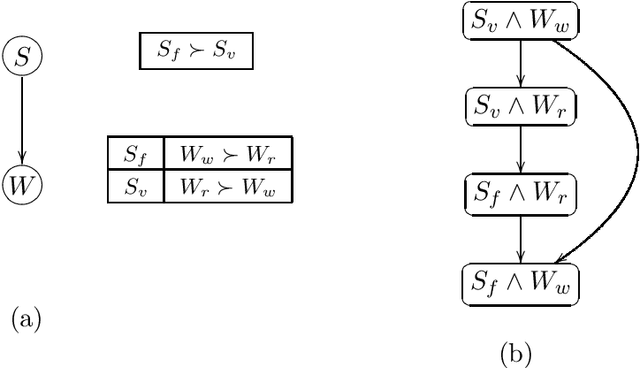
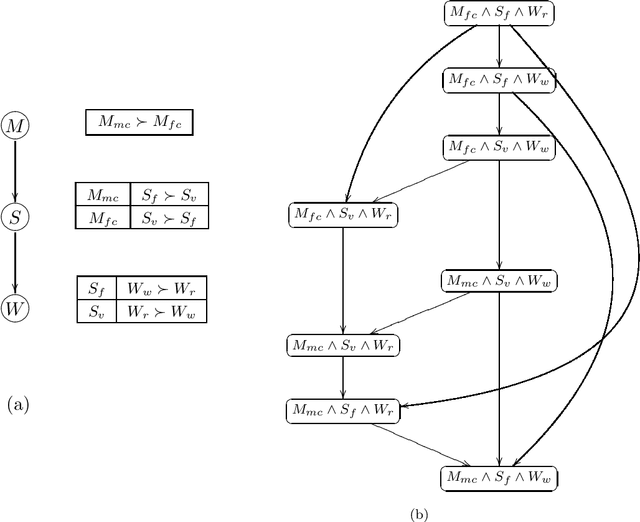
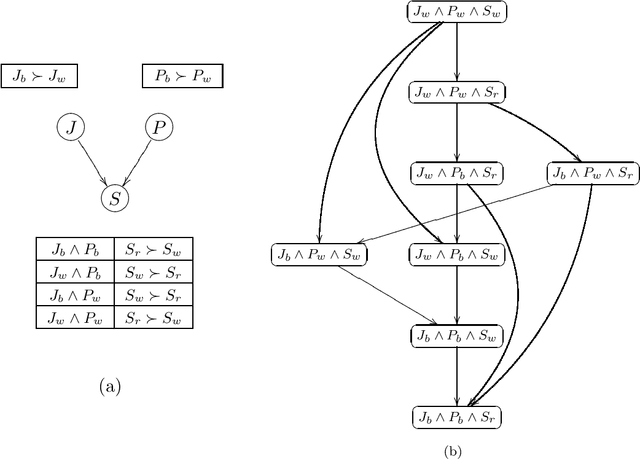
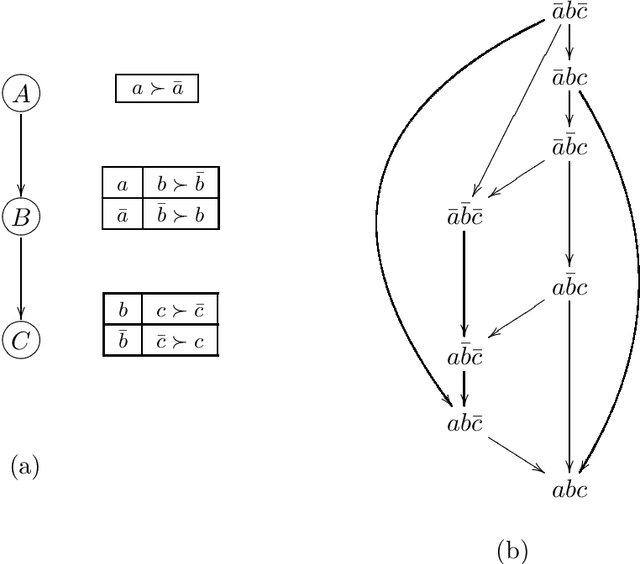
Information about user preferences plays a key role in automated decision making. In many domains it is desirable to assess such preferences in a qualitative rather than quantitative way. In this paper, we propose a qualitative graphical representation of preferences that reflects conditional dependence and independence of preference statements under a ceteris paribus (all else being equal) interpretation. Such a representation is often compact and arguably quite natural in many circumstances. We provide a formal semantics for this model, and describe how the structure of the network can be exploited in several inference tasks, such as determining whether one outcome dominates (is preferred to) another, ordering a set outcomes according to the preference relation, and constructing the best outcome subject to available evidence.