Restoring balance: principled under/oversampling of data for optimal classification

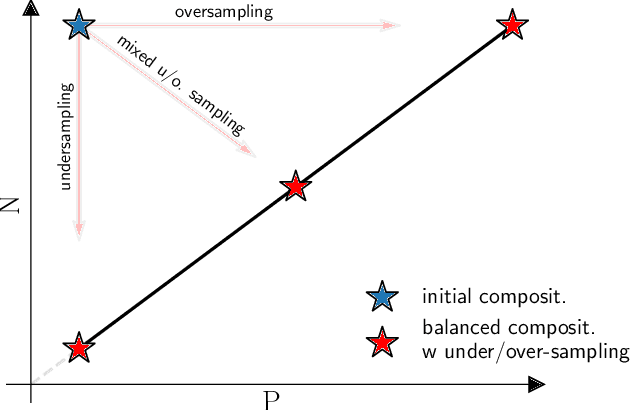
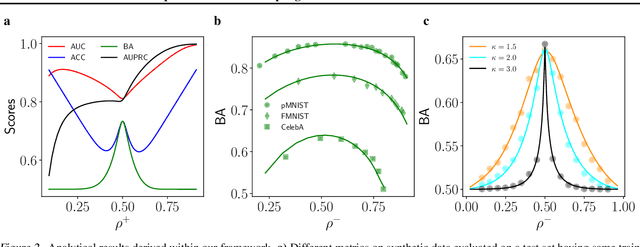
Class imbalance in real-world data poses a common bottleneck for machine learning tasks, since achieving good generalization on under-represented examples is often challenging. Mitigation strategies, such as under or oversampling the data depending on their abundances, are routinely proposed and tested empirically, but how they should adapt to the data statistics remains poorly understood. In this work, we determine exact analytical expressions of the generalization curves in the high-dimensional regime for linear classifiers (Support Vector Machines). We also provide a sharp prediction of the effects of under/oversampling strategies depending on class imbalance, first and second moments of the data, and the metrics of performance considered. We show that mixed strategies involving under and oversampling of data lead to performance improvement. Through numerical experiments, we show the relevance of our theoretical predictions on real datasets, on deeper architectures and with sampling strategies based on unsupervised probabilistic models.

Low-Dimensional Manifolds Support Multiplexed Integrations in Recurrent Neural Networks

We study the learning dynamics and the representations emerging in Recurrent Neural Networks trained to integrate one or multiple temporal signals. Combining analytical and numerical investigations, we characterize the conditions under which a RNN with n neurons learns to integrate D(n) scalar signals of arbitrary duration. We show, both for linear and ReLU neurons, that its internal state lives close to a D-dimensional manifold, whose shape is related to the activation function. Each neuron therefore carries, to various degrees, information about the value of all integrals. We discuss the deep analogy between our results and the concept of mixed selectivity forged by computational neuroscientists to interpret cortical recordings.

Learning Compositional Representations of Interacting Systems with Restricted Boltzmann Machines: Comparative Study of Lattice Proteins

A Restricted Boltzmann Machine (RBM) is an unsupervised machine-learning bipartite graphical model that jointly learns a probability distribution over data and extracts their relevant statistical features. As such, RBM were recently proposed for characterizing the patterns of coevolution between amino acids in protein sequences and for designing new sequences. Here, we study how the nature of the features learned by RBM changes with its defining parameters, such as the dimensionality of the representations (size of the hidden layer) and the sparsity of the features. We show that for adequate values of these parameters, RBM operate in a so-called compositional phase in which visible configurations sampled from the RBM are obtained by recombining these features. We then compare the performance of RBM with other standard representation learning algorithms, including Principal or Independent Component Analysis, autoencoders (AE), variational auto-encoders (VAE), and their sparse variants. We show that RBM, due to the stochastic mapping between data configurations and representations, better capture the underlying interactions in the system and are significantly more robust with respect to sample size than deterministic methods such as PCA or ICA. In addition, this stochastic mapping is not prescribed a priori as in VAE, but learned from data, which allows RBM to show good performance even with shallow architectures. All numerical results are illustrated on synthetic lattice-protein data, that share similar statistical features with real protein sequences, and for which ground-truth interactions are known.

Emergence of Compositional Representations in Restricted Boltzmann Machines

Extracting automatically the complex set of features composing real high-dimensional data is crucial for achieving high performance in machine--learning tasks. Restricted Boltzmann Machines (RBM) are empirically known to be efficient for this purpose, and to be able to generate distributed and graded representations of the data. We characterize the structural conditions (sparsity of the weights, low effective temperature, nonlinearities in the activation functions of hidden units, and adaptation of fields maintaining the activity in the visible layer) allowing RBM to operate in such a compositional phase. Evidence is provided by the replica analysis of an adequate statistical ensemble of random RBMs and by RBM trained on the handwritten digits dataset MNIST.

Adaptive Cluster Expansion for Inferring Boltzmann Machines with Noisy Data

We introduce a procedure to infer the interactions among a set of binary variables, based on their sampled frequencies and pairwise correlations. The algorithm builds the clusters of variables contributing most to the entropy of the inferred Ising model, and rejects the small contributions due to the sampling noise. Our procedure successfully recovers benchmark Ising models even at criticality and in the low temperature phase, and is applied to neurobiological data.