EXAGREE: Towards Explanation Agreement in Explainable Machine Learning

Explanations in machine learning are critical for trust, transparency, and fairness. Yet, complex disagreements among these explanations limit the reliability and applicability of machine learning models, especially in high-stakes environments. We formalize four fundamental ranking-based explanation disagreement problems and introduce a novel framework, EXplanation AGREEment (EXAGREE), to bridge diverse interpretations in explainable machine learning, particularly from stakeholder-centered perspectives. Our approach leverages a Rashomon set for attribution predictions and then optimizes within this set to identify Stakeholder-Aligned Explanation Models (SAEMs) that minimize disagreement with diverse stakeholder needs while maintaining predictive performance. Rigorous empirical analysis on synthetic and real-world datasets demonstrates that EXAGREE reduces explanation disagreement and improves fairness across subgroups in various domains. EXAGREE not only provides researchers with a new direction for studying explanation disagreement problems but also offers data scientists a tool for making better-informed decisions in practical applications.

Practical Attribution Guidance for Rashomon Sets

Different prediction models might perform equally well (Rashomon set) in the same task, but offer conflicting interpretations and conclusions about the data. The Rashomon effect in the context of Explainable AI (XAI) has been recognized as a critical factor. Although the Rashomon set has been introduced and studied in various contexts, its practical application is at its infancy stage and lacks adequate guidance and evaluation. We study the problem of the Rashomon set sampling from a practical viewpoint and identify two fundamental axioms - generalizability and implementation sparsity that exploring methods ought to satisfy in practical usage. These two axioms are not satisfied by most known attribution methods, which we consider to be a fundamental weakness. We use the norms to guide the design of an $\epsilon$-subgradient-based sampling method. We apply this method to a fundamental mathematical problem as a proof of concept and to a set of practical datasets to demonstrate its ability compared with existing sampling methods.

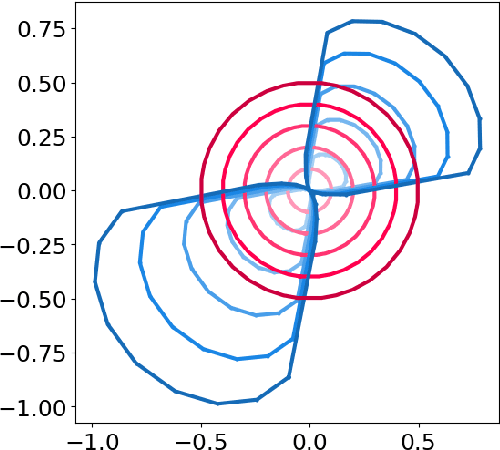
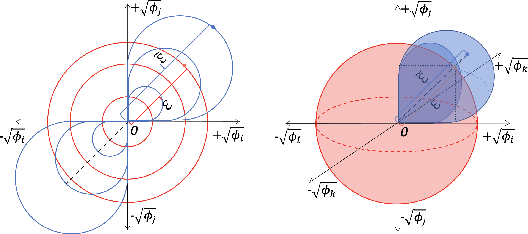
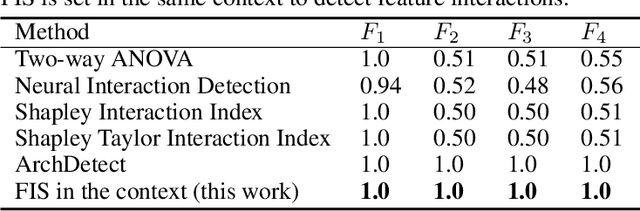
Exploring the cloud of feature interaction scores in a Rashomon set

Interactions among features are central to understanding the behavior of machine learning models. Recent research has made significant strides in detecting and quantifying feature interactions in single predictive models. However, we argue that the feature interactions extracted from a single pre-specified model may not be trustworthy since: a well-trained predictive model may not preserve the true feature interactions and there exist multiple well-performing predictive models that differ in feature interaction strengths. Thus, we recommend exploring feature interaction strengths in a model class of approximately equally accurate predictive models. In this work, we introduce the feature interaction score (FIS) in the context of a Rashomon set, representing a collection of models that achieve similar accuracy on a given task. We propose a general and practical algorithm to calculate the FIS in the model class. We demonstrate the properties of the FIS via synthetic data and draw connections to other areas of statistics. Additionally, we introduce a Halo plot for visualizing the feature interaction variance in high-dimensional space and a swarm plot for analyzing FIS in a Rashomon set. Experiments with recidivism prediction and image classification illustrate how feature interactions can vary dramatically in importance for similarly accurate predictive models. Our results suggest that the proposed FIS can provide valuable insights into the nature of feature interactions in machine learning models.

Physics-Informed Neural Networks for Discovering Localised Eigenstates in Disordered Media

The Schr\"{o}dinger equation with random potentials is a fundamental model for understanding the behaviour of particles in disordered systems. Disordered media are characterised by complex potentials that lead to the localisation of wavefunctions, also called Anderson localisation. These wavefunctions may have similar scales of eigenenergies which poses difficulty in their discovery. It has been a longstanding challenge due to the high computational cost and complexity of solving the Schr\"{o}dinger equation. Recently, machine-learning tools have been adopted to tackle these challenges. In this paper, based upon recent advances in machine learning, we present a novel approach for discovering localised eigenstates in disordered media using physics-informed neural networks (PINNs). We focus on the spectral approximation of Hamiltonians in one dimension with potentials that are randomly generated according to the Bernoulli, normal, and uniform distributions. We introduce a novel feature to the loss function that exploits known physical phenomena occurring in these regions to scan across the domain and successfully discover these eigenstates, regardless of the similarity of their eigenenergies. We present various examples to demonstrate the performance of the proposed approach and compare it with isogeometric analysis.