Incremental Nonlinear Fault-Tolerant Control of a Quadrotor with Complete Loss of Two Opposing Rotors

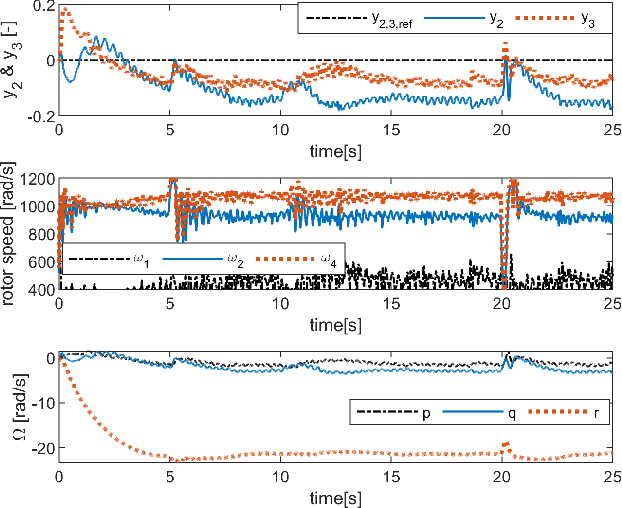
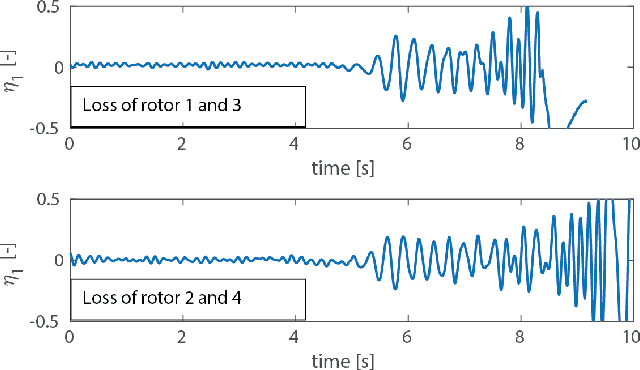
In order to further expand the flight envelope of quadrotors under actuator failures, we design a nonlinear sensor-based fault-tolerant controller to stabilize a quadrotor with failure of two opposing rotors in the high-speed flight condition (> 8m/s). The incremental nonlinear dynamic inversion (INDI) approach which excels in handling model uncertainties is adopted to compensate for the significant unknown aerodynamic effects. The internal dynamics of such an underactuated system have been analyzed, and subsequently stabilized by re-defining the control output. The proposed method can be generalized to control a quadrotor under single-rotor-failure and nominal conditions. For validation, flight tests have been carried out in a large-scale open jet wind tunnel. The position of a damaged quadrotor can be controlled in the presence of significant wind disturbances. A linear quadratic regulator (LQR) approach from the literature has been compared to demonstrate the advantages of the proposed nonlinear method in the windy and high-speed flight condition.

Cascaded Incremental Nonlinear Dynamic Inversion Control for MAV Disturbance Rejection

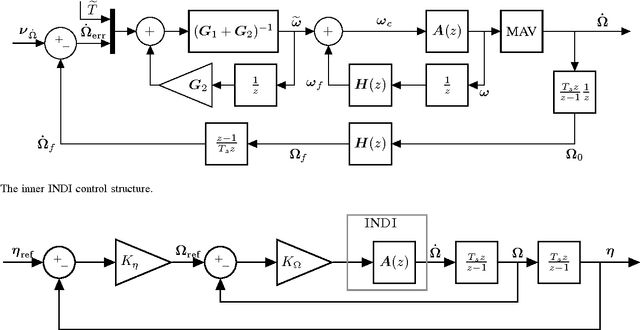
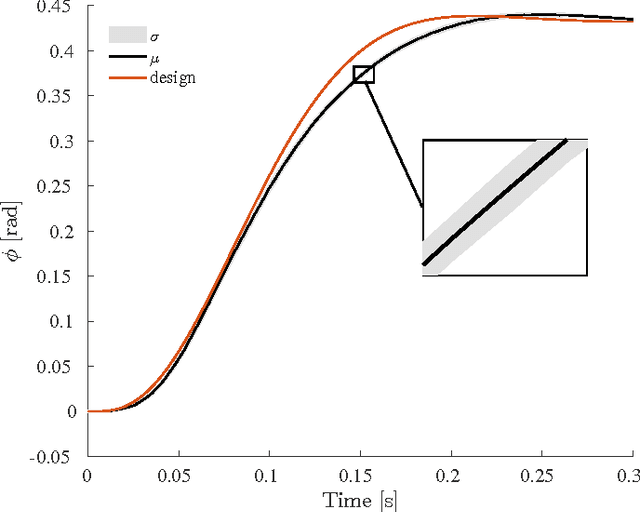
Micro Aerial Vehicles (MAVs) are limited in their operation outdoors near obstacles by their ability to withstand wind gusts. Currently widespread position control methods such as Proportional Integral Derivative control do not perform well under the influence of gusts. Incremental Nonlinear Dynamic Inversion (INDI) is a sensor-based control technique that can control nonlinear systems subject to disturbances. It was developed for the attitude control of manned aircraft or MAVs. In this paper we generalize this method to the outer loop control of MAVs under severe gust loads. Significant improvements over a traditional Proportional Integral Derivative (PID) controller are demonstrated in an experiment where the quadrotor flies in and out of a windtunnel exhaust at 10 m/s. The control method does not rely on frequent position updates, as is demonstrated in an outside experiment using a standard GPS module. Finally, we investigate the effect of using a linearization to calculate thrust vector increments, compared to a nonlinear calculation. The method requires little modeling and is computationally efficient.