LeetDecoding: A PyTorch Library for Exponentially Decaying Causal Linear Attention with CUDA Implementations

The machine learning and data science community has made significant while dispersive progress in accelerating transformer-based large language models (LLMs), and one promising approach is to replace the original causal attention in a generative pre-trained transformer (GPT) with \emph{exponentially decaying causal linear attention}. In this paper, we present LeetDecoding, which is the first Python package that provides a large set of computation routines for this fundamental operator. The launch of LeetDecoding was motivated by the current lack of (1) clear understanding of the complexity regarding this operator, (2) a comprehensive collection of existing computation methods (usually spread in seemingly unrelated fields), and (3) CUDA implementations for fast inference on GPU. LeetDecoding's design is easy to integrate with existing linear-attention LLMs, and allows for researchers to benchmark and evaluate new computation methods for exponentially decaying causal linear attention. The usage of LeetDecoding does not require any knowledge of GPU programming and the underlying complexity analysis, intentionally making LeetDecoding accessible to LLM practitioners. The source code of LeetDecoding is provided at \href{https://github.com/Computational-Machine-Intelligence/LeetDecoding}{this GitHub repository}, and users can simply install LeetDecoding by the command \texttt{pip install leet-decoding}.

Implicit Regularization via Hadamard Product Over-Parametrization in High-Dimensional Linear Regression

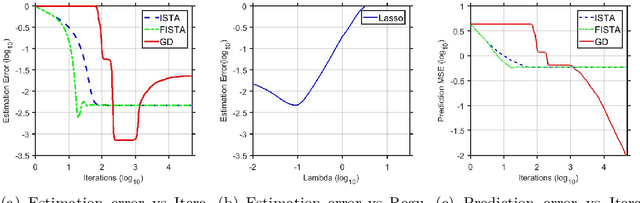
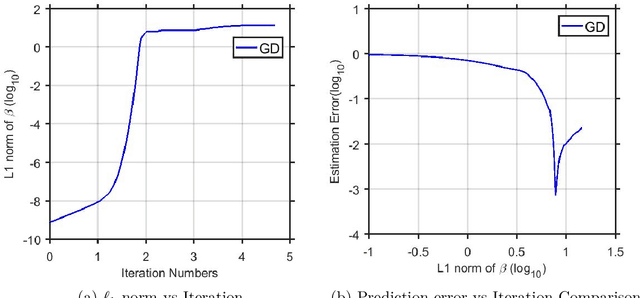
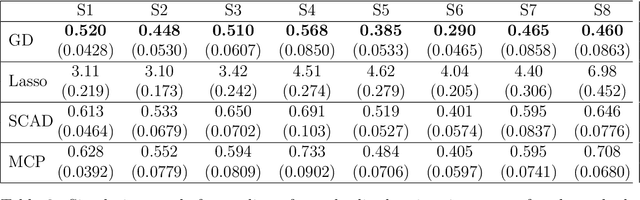
We consider Hadamard product parametrization as a change-of-variable (over-parametrization) technique for solving least square problems in the context of linear regression. Despite the non-convexity and exponentially many saddle points induced by the change-of-variable, we show that under certain conditions, this over-parametrization leads to implicit regularization: if we directly apply gradient descent to the residual sum of squares with sufficiently small initial values, then under proper early stopping rule, the iterates converge to a nearly sparse rate-optimal solution with relatively better accuracy than explicit regularized approaches. In particular, the resulting estimator does not suffer from extra bias due to explicit penalties, and can achieve the parametric root-$n$ rate (independent of the dimension) under proper conditions on the signal-to-noise ratio. We perform simulations to compare our methods with high dimensional linear regression with explicit regularizations. Our results illustrate advantages of using implicit regularization via gradient descent after over-parametrization in sparse vector estimation.