Implicit Regularization via Hadamard Product Over-Parametrization in High-Dimensional Linear Regression

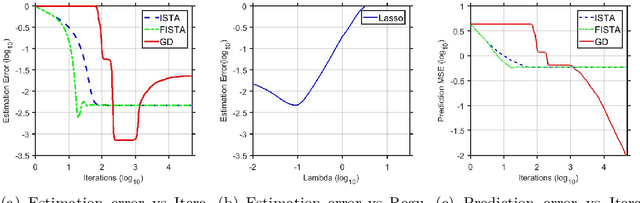
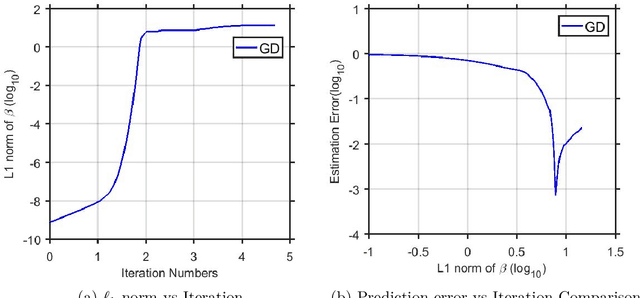
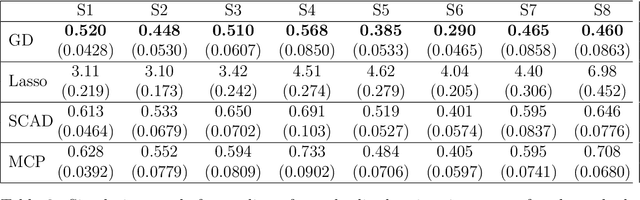
We consider Hadamard product parametrization as a change-of-variable (over-parametrization) technique for solving least square problems in the context of linear regression. Despite the non-convexity and exponentially many saddle points induced by the change-of-variable, we show that under certain conditions, this over-parametrization leads to implicit regularization: if we directly apply gradient descent to the residual sum of squares with sufficiently small initial values, then under proper early stopping rule, the iterates converge to a nearly sparse rate-optimal solution with relatively better accuracy than explicit regularized approaches. In particular, the resulting estimator does not suffer from extra bias due to explicit penalties, and can achieve the parametric root-$n$ rate (independent of the dimension) under proper conditions on the signal-to-noise ratio. We perform simulations to compare our methods with high dimensional linear regression with explicit regularizations. Our results illustrate advantages of using implicit regularization via gradient descent after over-parametrization in sparse vector estimation.