A novel multi-scale loss function for classification problems in machine learning

We introduce two-scale loss functions for use in various gradient descent algorithms applied to classification problems via deep neural networks. This new method is generic in the sense that it can be applied to a wide range of machine learning architectures, from deep neural networks to support vector machines for example. These two-scale loss functions allow to focus the training onto objects in the training set which are not well classified. This leads to an increase in several measures of performance for appropriately-defined two-scale loss functions with respect to the more classical cross-entropy when tested on traditional deep neural networks on the MNIST, CIFAR10, and CIFAR100 data-sets.

Stability for the Training of Deep Neural Networks and Other Classifiers

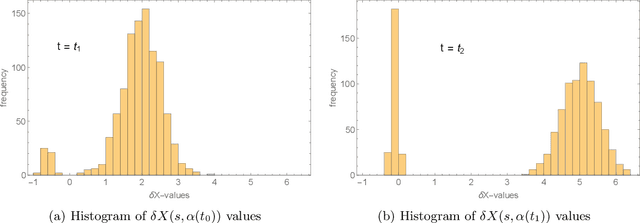
We examine the stability of loss-minimizing training processes that are used for deep neural network (DNN) and other classifiers. While a classifier is optimized during training through a so-called loss function, the performance of classifiers is usually evaluated by some measure of accuracy, such as the overall accuracy which quantifies the proportion of objects that are well classified. This leads to the guiding question of stability: does decreasing loss through training always result in increased accuracy? We formalize the notion of stability, and provide examples of instability. Our main result is two novel conditions on the classifier which, if either is satisfied, ensure stability of training, that is we derive tight bounds on accuracy as loss decreases. These conditions are explicitly verifiable in practice on a given dataset. Our results do not depend on the algorithm used for training, as long as loss decreases with training.

Transport Model for Feature Extraction

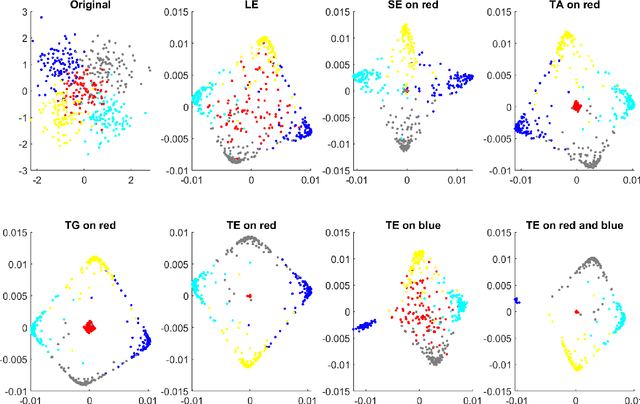
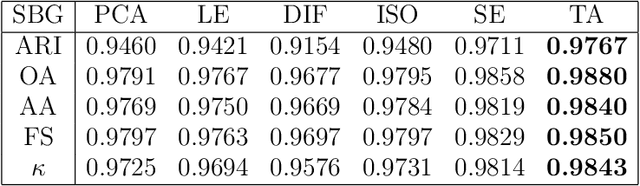
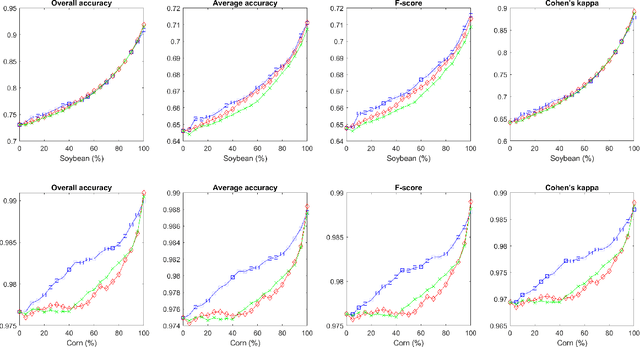
We present a new feature extraction method for complex and large datasets, based on the concept of transport operators on graphs. The proposed approach generalizes and extends the many existing data representation methodologies built upon diffusion processes, to a new domain where dynamical systems play a key role. The main advantage of this approach comes from the ability to exploit different relationships than those arising in the context of e.g., Graph Laplacians. Fundamental properties of the transport operators are proved. We demonstrate the flexibility of the method by introducing several diverse examples of transformations. We close the paper with a series of computational experiments and applications to the problem of classification of hyperspectral satellite imagery, to illustrate the practical implications of our algorithm and its ability to quantify new aspects of relationships within complicated datasets.