Autoregressive Convolutional Neural Networks for Asynchronous Time Series

We propose Significance-Offset Convolutional Neural Network, a deep convolutional network architecture for regression of multivariate asynchronous time series. The model is inspired by standard autoregressive (AR) models and gating mechanisms used in recurrent neural networks. It involves an AR-like weighting system, where the final predictor is obtained as a weighted sum of adjusted regressors, while the weights are datadependent functions learnt through a convolutional network. The architecture was designed for applications on asynchronous time series and is evaluated on such datasets: a hedge fund proprietary dataset of over 2 million quotes for a credit derivative index, an artificially generated noisy autoregressive series and UCI household electricity consumption dataset. The proposed architecture achieves promising results as compared to convolutional and recurrent neural networks.

Putting Self-Supervised Token Embedding on the Tables

Information distribution by electronic messages is a privileged means of transmission for many businesses and individuals, often under the form of plain-text tables. As their number grows, it becomes necessary to use an algorithm to extract text and numbers instead of a human. Usual methods are focused on regular expressions or on a strict structure in the data, but are not efficient when we have many variations, fuzzy structure or implicit labels. In this paper we introduce SC2T, a totally self-supervised model for constructing vector representations of tokens in semi-structured messages by using characters and context levels that address these issues. It can then be used for an unsupervised labeling of tokens, or be the basis for a semi-supervised information extraction system.

Optimal Transport vs. Fisher-Rao distance between Copulas for Clustering Multivariate Time Series

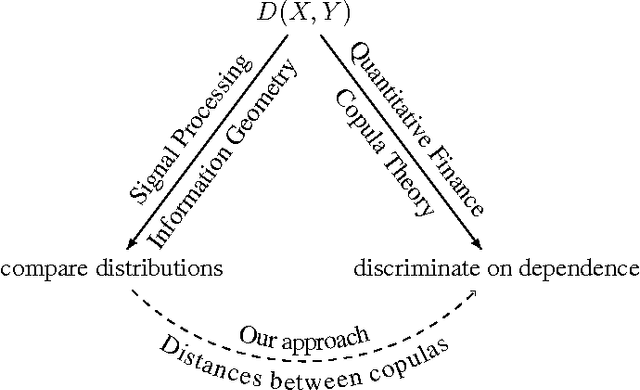
We present a methodology for clustering N objects which are described by multivariate time series, i.e. several sequences of real-valued random variables. This clustering methodology leverages copulas which are distributions encoding the dependence structure between several random variables. To take fully into account the dependence information while clustering, we need a distance between copulas. In this work, we compare renowned distances between distributions: the Fisher-Rao geodesic distance, related divergences and optimal transport, and discuss their advantages and disadvantages. Applications of such methodology can be found in the clustering of financial assets. A tutorial, experiments and implementation for reproducible research can be found at www.datagrapple.com/Tech.

Exploring and measuring non-linear correlations: Copulas, Lightspeed Transportation and Clustering

We propose a methodology to explore and measure the pairwise correlations that exist between variables in a dataset. The methodology leverages copulas for encoding dependence between two variables, state-of-the-art optimal transport for providing a relevant geometry to the copulas, and clustering for summarizing the main dependence patterns found between the variables. Some of the clusters centers can be used to parameterize a novel dependence coefficient which can target or forget specific dependence patterns. Finally, we illustrate and benchmark the methodology on several datasets. Code and numerical experiments are available online for reproducible research.

Clustering Financial Time Series: How Long is Enough?

Researchers have used from 30 days to several years of daily returns as source data for clustering financial time series based on their correlations. This paper sets up a statistical framework to study the validity of such practices. We first show that clustering correlated random variables from their observed values is statistically consistent. Then, we also give a first empirical answer to the much debated question: How long should the time series be? If too short, the clusters found can be spurious; if too long, dynamics can be smoothed out.

Optimal Copula Transport for Clustering Multivariate Time Series

This paper presents a new methodology for clustering multivariate time series leveraging optimal transport between copulas. Copulas are used to encode both (i) intra-dependence of a multivariate time series, and (ii) inter-dependence between two time series. Then, optimal copula transport allows us to define two distances between multivariate time series: (i) one for measuring intra-dependence dissimilarity, (ii) another one for measuring inter-dependence dissimilarity based on a new multivariate dependence coefficient which is robust to noise, deterministic, and which can target specified dependencies.

Toward a generic representation of random variables for machine learning

This paper presents a pre-processing and a distance which improve the performance of machine learning algorithms working on independent and identically distributed stochastic processes. We introduce a novel non-parametric approach to represent random variables which splits apart dependency and distribution without losing any information. We also propound an associated metric leveraging this representation and its statistical estimate. Besides experiments on synthetic datasets, the benefits of our contribution is illustrated through the example of clustering financial time series, for instance prices from the credit default swaps market. Results are available on the website www.datagrapple.com and an IPython Notebook tutorial is available at www.datagrapple.com/Tech for reproducible research.