Optimal Transport vs. Fisher-Rao distance between Copulas for Clustering Multivariate Time Series

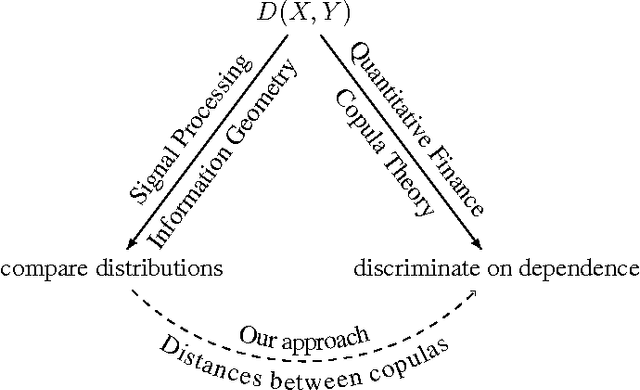
We present a methodology for clustering N objects which are described by multivariate time series, i.e. several sequences of real-valued random variables. This clustering methodology leverages copulas which are distributions encoding the dependence structure between several random variables. To take fully into account the dependence information while clustering, we need a distance between copulas. In this work, we compare renowned distances between distributions: the Fisher-Rao geodesic distance, related divergences and optimal transport, and discuss their advantages and disadvantages. Applications of such methodology can be found in the clustering of financial assets. A tutorial, experiments and implementation for reproducible research can be found at www.datagrapple.com/Tech.

Clustering Financial Time Series: How Long is Enough?

Researchers have used from 30 days to several years of daily returns as source data for clustering financial time series based on their correlations. This paper sets up a statistical framework to study the validity of such practices. We first show that clustering correlated random variables from their observed values is statistically consistent. Then, we also give a first empirical answer to the much debated question: How long should the time series be? If too short, the clusters found can be spurious; if too long, dynamics can be smoothed out.