Compressive Imaging and Characterization of Sparse Light Deflection Maps

Light rays incident on a transparent object of uniform refractive index undergo deflections, which uniquely characterize the surface geometry of the object. Associated with each point on the surface is a deflection map (or spectrum) which describes the pattern of deflections in various directions. This article presents a novel method to efficiently acquire and reconstruct sparse deflection spectra induced by smooth object surfaces. To this end, we leverage the framework of Compressed Sensing (CS) in a particular implementation of a schlieren deflectometer, i.e., an optical system providing linear measurements of deflection spectra with programmable spatial light modulation patterns. We design those modulation patterns on the principle of spread spectrum CS for reducing the number of observations. The ability of our device to simultaneously observe the deflection spectra on a dense discretization of the object surface is related to a Multiple Measurement Vector (MMV) model. This scheme allows us to estimate both the noise power and the instrumental point spread function. We formulate the spectrum reconstruction task as the solving of a linear inverse problem regularized by an analysis sparsity prior using a translation invariant wavelet frame. Our results demonstrate the capability and advantages of using a CS based approach for deflectometric imaging both on simulated data and experimental deflectometric data. Finally, the paper presents an extension of our method showing how we can extract the main deflection direction in each point of the object surface from a few compressive measurements, without needing any costly reconstruction procedures. This compressive characterization is then confirmed with experimental results on simple plano-convex and multifocal intra-ocular lenses studying the evolution of the main deflection as a function of the object point location.

Compressive Optical Deflectometric Tomography: A Constrained Total-Variation Minimization Approach

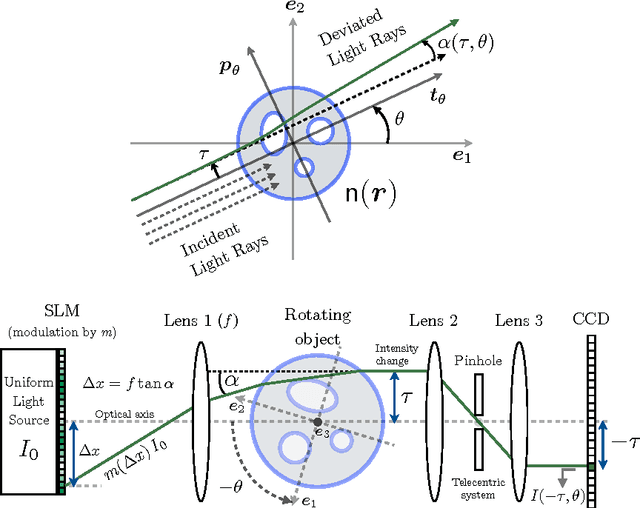
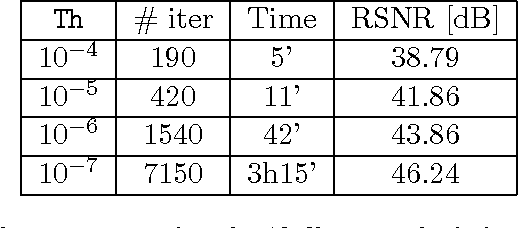
Optical Deflectometric Tomography (ODT) provides an accurate characterization of transparent materials whose complex surfaces present a real challenge for manufacture and control. In ODT, the refractive index map (RIM) of a transparent object is reconstructed by measuring light deflection under multiple orientations. We show that this imaging modality can be made "compressive", i.e., a correct RIM reconstruction is achievable with far less observations than required by traditional Filtered Back Projection (FBP) methods. Assuming a cartoon-shape RIM model, this reconstruction is driven by minimizing the map Total-Variation under a fidelity constraint with the available observations. Moreover, two other realistic assumptions are added to improve the stability of our approach: the map positivity and a frontier condition. Numerically, our method relies on an accurate ODT sensing model and on a primal-dual minimization scheme, including easily the sensing operator and the proposed RIM constraints. We conclude this paper by demonstrating the power of our method on synthetic and experimental data under various compressive scenarios. In particular, the compressiveness of the stabilized ODT problem is demonstrated by observing a typical gain of 20 dB compared to FBP at only 5% of 360 incident light angles for moderately noisy sensing.

Compressive Schlieren Deflectometry

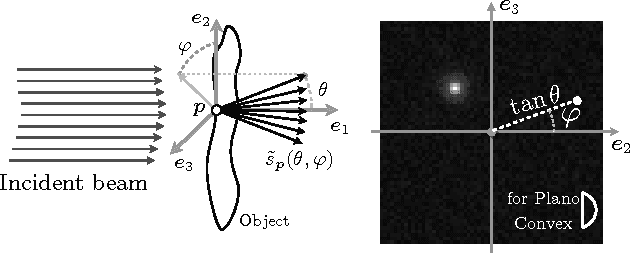
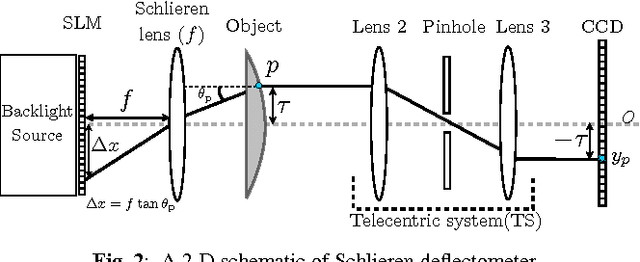
Schlieren deflectometry aims at characterizing the deflections undergone by refracted incident light rays at any surface point of a transparent object. For smooth surfaces, each surface location is actually associated with a sparse deflection map (or spectrum). This paper presents a novel method to compressively acquire and reconstruct such spectra. This is achieved by altering the way deflection information is captured in a common Schlieren Deflectometer, i.e., the deflection spectra are indirectly observed by the principle of spread spectrum compressed sensing. These observations are realized optically using a 2-D Spatial Light Modulator (SLM) adjusted to the corresponding sensing basis and whose modulations encode the light deviation subsequently recorded by a CCD camera. The efficiency of this approach is demonstrated experimentally on the observation of few test objects. Further, using a simple parametrization of the deflection spectra we show that relevant key parameters can be directly computed using the measurements, avoiding full reconstruction.