Multi-resolution Compressive Sensing Reconstruction

We consider the problem of reconstructing an image from compressive measurements using a multi-resolution grid. In this context, the reconstructed image is divided into multiple regions, each one with a different resolution. This problem arises in situations where the image to reconstruct contains a certain region of interest (RoI) that is more important than the rest. Through a theoretical analysis and simulation experiments we show that the multi-resolution reconstruction provides a higher quality of the RoI compared to the traditional single-resolution approach.

Non-parametric PSF estimation from celestial transit solar images using blind deconvolution

Context: Characterization of instrumental effects in astronomical imaging is important in order to extract accurate physical information from the observations. The measured image in a real optical instrument is usually represented by the convolution of an ideal image with a Point Spread Function (PSF). Additionally, the image acquisition process is also contaminated by other sources of noise (read-out, photon-counting). The problem of estimating both the PSF and a denoised image is called blind deconvolution and is ill-posed. Aims: We propose a blind deconvolution scheme that relies on image regularization. Contrarily to most methods presented in the literature, our method does not assume a parametric model of the PSF and can thus be applied to any telescope. Methods: Our scheme uses a wavelet analysis prior model on the image and weak assumptions on the PSF. We use observations from a celestial transit, where the occulting body can be assumed to be a black disk. These constraints allow us to retain meaningful solutions for the filter and the image, eliminating trivial, translated and interchanged solutions. Under an additive Gaussian noise assumption, they also enforce noise canceling and avoid reconstruction artifacts by promoting the whiteness of the residual between the blurred observations and the cleaned data. Results: Our method is applied to synthetic and experimental data. The PSF is estimated for the SECCHI/EUVI instrument using the 2007 Lunar transit, and for SDO/AIA using the 2012 Venus transit. Results show that the proposed non-parametric blind deconvolution method is able to estimate the core of the PSF with a similar quality to parametric methods proposed in the literature. We also show that, if these parametric estimations are incorporated in the acquisition model, the resulting PSF outperforms both the parametric and non-parametric methods.

Compressive Optical Deflectometric Tomography: A Constrained Total-Variation Minimization Approach

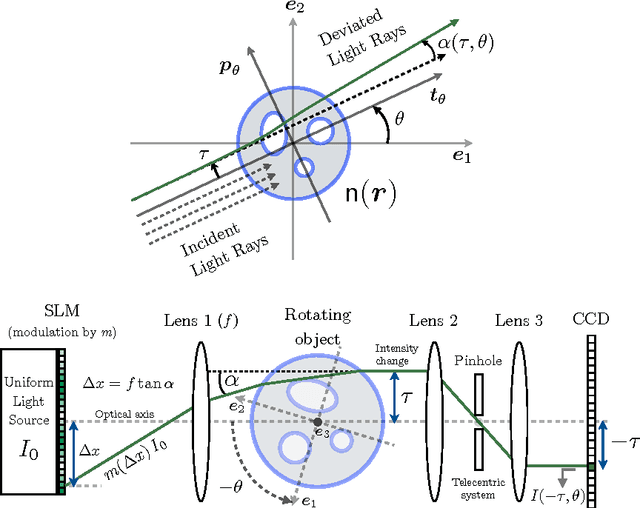
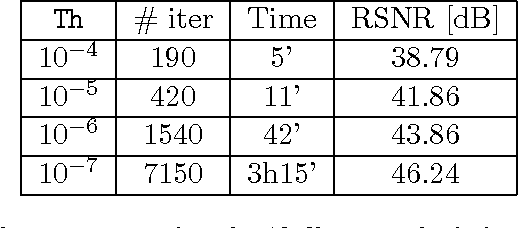
Optical Deflectometric Tomography (ODT) provides an accurate characterization of transparent materials whose complex surfaces present a real challenge for manufacture and control. In ODT, the refractive index map (RIM) of a transparent object is reconstructed by measuring light deflection under multiple orientations. We show that this imaging modality can be made "compressive", i.e., a correct RIM reconstruction is achievable with far less observations than required by traditional Filtered Back Projection (FBP) methods. Assuming a cartoon-shape RIM model, this reconstruction is driven by minimizing the map Total-Variation under a fidelity constraint with the available observations. Moreover, two other realistic assumptions are added to improve the stability of our approach: the map positivity and a frontier condition. Numerically, our method relies on an accurate ODT sensing model and on a primal-dual minimization scheme, including easily the sensing operator and the proposed RIM constraints. We conclude this paper by demonstrating the power of our method on synthetic and experimental data under various compressive scenarios. In particular, the compressiveness of the stabilized ODT problem is demonstrated by observing a typical gain of 20 dB compared to FBP at only 5% of 360 incident light angles for moderately noisy sensing.