Sparse Bayesian Learning for Label Efficiency in Cardiac Real-Time MRI

Cardiac real-time magnetic resonance imaging (MRI) is an emerging technology that images the heart at up to 50 frames per second, offering insight into the respiratory effects on the heartbeat. However, this method significantly increases the number of images that must be segmented to derive critical health indicators. Although neural networks perform well on inner slices, predictions on outer slices are often unreliable. This work proposes sparse Bayesian learning (SBL) to predict the ventricular volume on outer slices with minimal manual labeling to address this challenge. The ventricular volume over time is assumed to be dominated by sparse frequencies corresponding to the heart and respiratory rates. Moreover, SBL identifies these sparse frequencies on well-segmented inner slices by optimizing hyperparameters via type -II likelihood, automatically pruning irrelevant components. The identified sparse frequencies guide the selection of outer slice images for labeling, minimizing posterior variance. This work provides performance guarantees for the greedy algorithm. Testing on patient data demonstrates that only a few labeled images are necessary for accurate volume prediction. The labeling procedure effectively avoids selecting inefficient images. Furthermore, the Bayesian approach provides uncertainty estimates, highlighting unreliable predictions (e.g., when choosing suboptimal labels).

FEM-based Neural Networks for Solving Incompressible Fluid Flows and Related Inverse Problems

The numerical simulation and optimization of technical systems described by partial differential equations is expensive, especially in multi-query scenarios in which the underlying equations have to be solved for different parameters. A comparatively new approach in this context is to combine the good approximation properties of neural networks (for parameter dependence) with the classical finite element method (for discretization). However, instead of considering the solution mapping of the PDE from the parameter space into the FEM-discretized solution space as a purely data-driven regression problem, so-called physically informed regression problems have proven to be useful. In these, the equation residual is minimized during the training of the neural network, i.e. the neural network "learns" the physics underlying the problem. In this paper, we extend this approach to saddle-point and non-linear fluid dynamics problems, respectively, namely stationary Stokes and stationary Navier-Stokes equations. In particular, we propose a modification of the existing approach: Instead of minimizing the plain vanilla equation residual during training, we minimize the equation residual modified by a preconditioner. By analogy with the linear case, this also improves the condition in the present non-linear case. Our numerical examples demonstrate that this approach significantly reduces the training effort and greatly increases accuracy and generalizability. Finally, we show the application of the resulting parameterized model to a related inverse problem.

HeAT -- a Distributed and GPU-accelerated Tensor Framework for Data Analytics

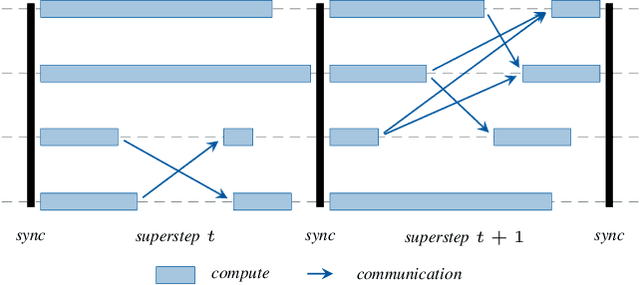
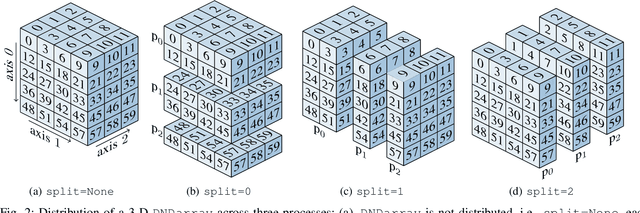
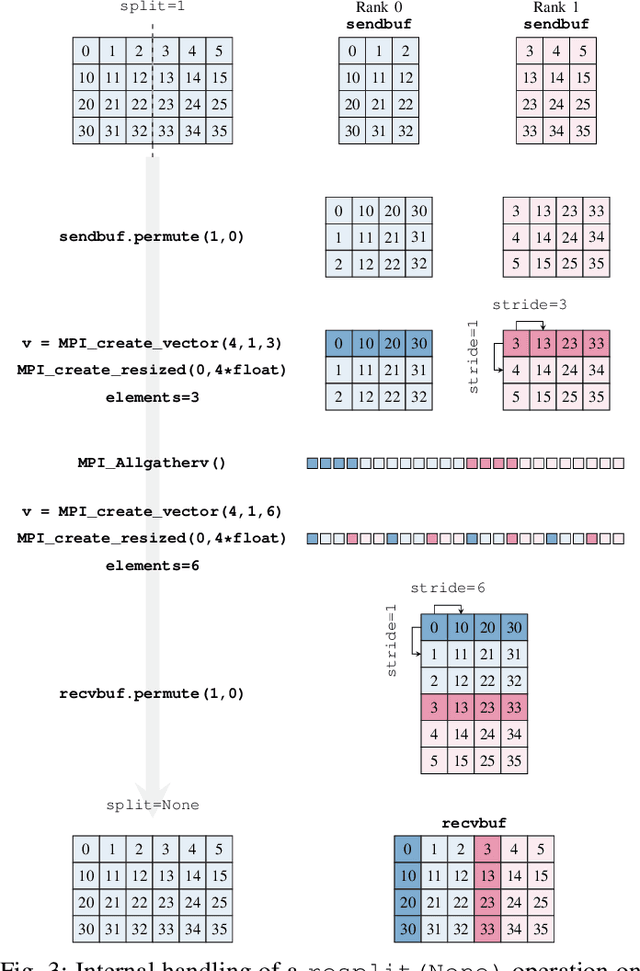
In order to cope with the exponential growth in available data, the efficiency of data analysis and machine learning libraries have recently received increased attention. Although corresponding array-based numerical kernels have been significantly improved, most are limited by the resources available on a single computational node. Consequently, kernels must exploit distributed resources, e.g., distributed memory architectures. To this end, we introduce HeAT, an array-based numerical programming framework for large-scale parallel processing with an easy-to-use NumPy-like API. HeAT utilizes PyTorch as a node-local eager execution engine and distributes the workload via MPI on arbitrarily large high-performance computing systems. It provides both low-level array-based computations, as well as assorted higher-level algorithms. With HeAT, it is possible for a NumPy user to take advantage of their available resources, significantly lowering the barrier to distributed data analysis. Compared with applications written in similar frameworks, HeAT achieves speedups of up to two orders of magnitude.