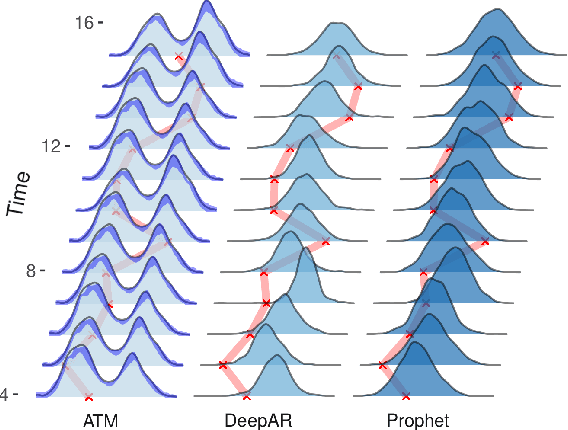
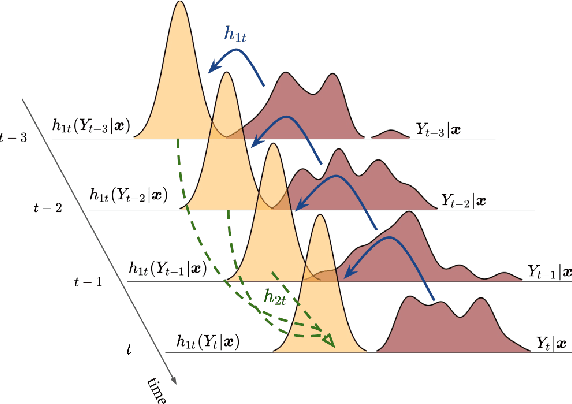
Transforming Autoregression: Interpretable and Expressive Time Series Forecast

Probabilistic forecasting of time series is an important matter in many applications and research fields. In order to draw conclusions from a probabilistic forecast, we must ensure that the model class used to approximate the true forecasting distribution is expressive enough. Yet, characteristics of the model itself, such as its uncertainty or its general functioning are not of lesser importance. In this paper, we propose Autoregressive Transformation Models (ATMs), a model class inspired from various research directions such as normalizing flows and autoregressive models. ATMs unite expressive distributional forecasts using a semi-parametric distribution assumption with an interpretable model specification and allow for uncertainty quantification based on (asymptotic) Maximum Likelihood theory. We demonstrate the properties of ATMs both theoretically and through empirical evaluation on several simulated and real-world forecasting datasets.

Translational Equivariance in Kernelizable Attention

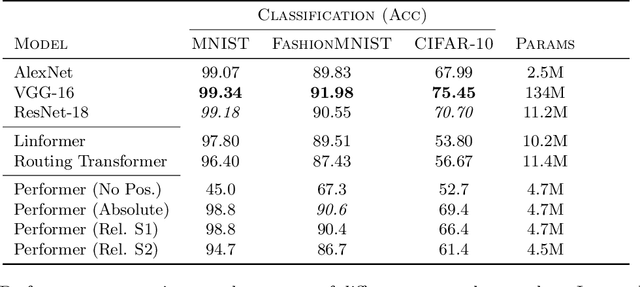
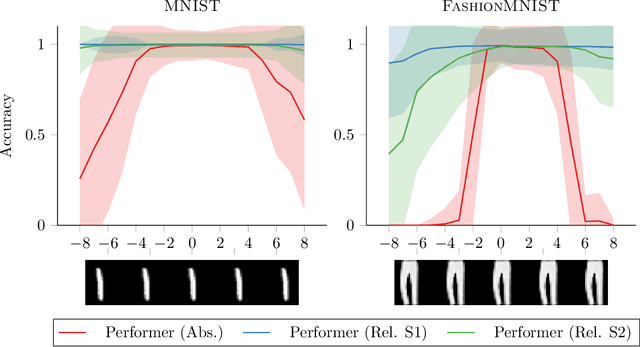
While Transformer architectures have show remarkable success, they are bound to the computation of all pairwise interactions of input element and thus suffer from limited scalability. Recent work has been successful by avoiding the computation of the complete attention matrix, yet leads to problems down the line. The absence of an explicit attention matrix makes the inclusion of inductive biases relying on relative interactions between elements more challenging. An extremely powerful inductive bias is translational equivariance, which has been conjectured to be responsible for much of the success of Convolutional Neural Networks on image recognition tasks. In this work we show how translational equivariance can be implemented in efficient Transformers based on kernelizable attention - Performers. Our experiments highlight that the devised approach significantly improves robustness of Performers to shifts of input images compared to their naive application. This represents an important step on the path of replacing Convolutional Neural Networks with more expressive Transformer architectures and will help to improve sample efficiency and robustness in this realm.

Deep Conditional Transformation Models

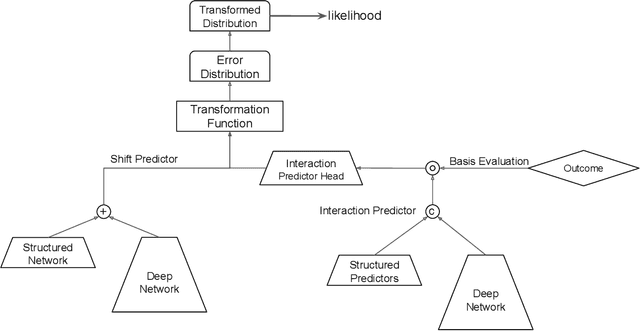
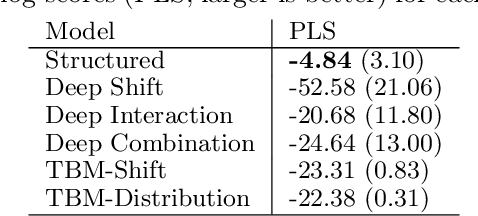
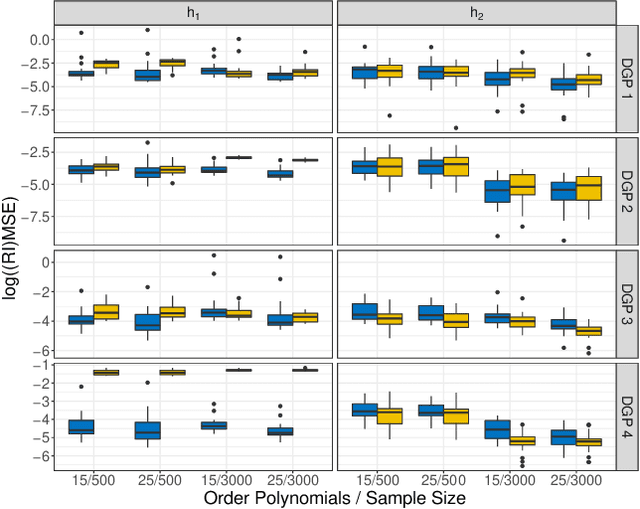
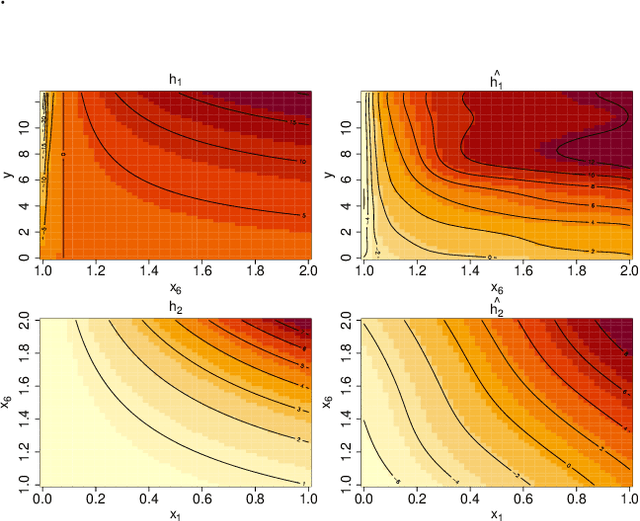
Learning the cumulative distribution function (CDF) of an outcome variable conditional on a set of features remains challenging, especially in high-dimensional settings. Conditional transformation models provide a semi-parametric approach that allows to model a large class of conditional CDFs without an explicit parametric distribution assumption and with only a few parameters. Existing estimation approaches within the class of transformation models are, however, either limited in their complexity and applicability to unstructured data sources such as images or text, or can incorporate complex effects of different features but lack interpretability. We close this gap by introducing the class of deep conditional transformation models which unify existing approaches and allow to learn both interpretable (non-)linear model terms and more complex predictors in one holistic neural network. To this end we propose a novel network architecture, provide details on different model definitions and derive suitable constraints and derive suitable network regularization terms. We demonstrate the efficacy of our approach through numerical experiments and applications.