Pragmatic information of aesthetic appraisal

A phenomenological model for aesthetic appraisal is proposed in terms of pragmatic information for a dynamic update semantics over belief states on an aesthetic appreciator. The model qualitatively correlates with aesthetic pleasure ratings in an experimental study on cadential effects in Western tonal music. Finally, related computational and neurodynamical accounts are discussed.

Invariants for neural automata

Computational modeling of neurodynamical systems often deploys neural networks and symbolic dynamics. A particular way for combining these approaches within a framework called vector symbolic architectures leads to neural automata. An interesting research direction we have pursued under this framework has been to consider mapping symbolic dynamics onto neurodynamics, represented as neural automata. This representation theory, enables us to ask questions, such as, how does the brain implement Turing computations. Specifically, in this representation theory, neural automata result from the assignment of symbols and symbol strings to numbers, known as G\"odel encoding. Under this assignment symbolic computation becomes represented by trajectories of state vectors in a real phase space, that allows for statistical correlation analyses with real-world measurements and experimental data. However, these assignments are usually completely arbitrary. Hence, it makes sense to address the problem question of, which aspects of the dynamics observed under such a representation is intrinsic to the dynamics and which are not. In this study, we develop a formally rigorous mathematical framework for the investigation of symmetries and invariants of neural automata under different encodings. As a central concept we define patterns of equality for such systems. We consider different macroscopic observables, such as the mean activation level of the neural network, and ask for their invariance properties. Our main result shows that only step functions that are defined over those patterns of equality are invariant under recodings, while the mean activation is not. Our work could be of substantial importance for related regression studies of real-world measurements with neurosymbolic processors for avoiding confounding results that are dependant on a particular encoding and not intrinsic to the dynamics.

Machine Semiotics

Despite their satisfactory speech recognition capabilities, current speech assistive devices still lack suitable automatic semantic analysis capabilities as well as useful representation of pragmatic world knowledge. Instead, current technologies require users to learn keywords necessary to effectively operate and work with a machine. Such a machine-centered approach can be frustrating for users. However, recognizing a basic difference between the semiotics of humans and machines presents a possibility to overcome this shortcoming: For the machine, the meaning of a (human) utterance is defined by its own scope of actions. Machines, thus, do not need to understand the meanings of individual words, nor the meaning of phrasal and sentence semantics that combine individual word meanings with additional implicit world knowledge. For speech assistive devices, the learning of machine specific meanings of human utterances by trial and error should be sufficient. Using the trivial example of a cognitive heating device, we show that -- based on dynamic semantics -- this process can be formalized as the learning of utterance-meaning pairs (UMP). This is followed by a detailed semiotic contextualization of the previously generated signs.

Reinforcement learning of minimalist grammars

Speech-controlled user interfaces facilitate the operation of devices and household functions to laymen. State-of-the-art language technology scans the acoustically analyzed speech signal for relevant keywords that are subsequently inserted into semantic slots to interpret the user's intent. In order to develop proper cognitive information and communication technologies, simple slot-filling should be replaced by utterance meaning transducers (UMT) that are based on semantic parsers and a mental lexicon, comprising syntactic, phonetic and semantic features of the language under consideration. This lexicon must be acquired by a cognitive agent during interaction with its users. We outline a reinforcement learning algorithm for the acquisition of syntax and semantics of English utterances, based on minimalist grammar (MG), a recent computational implementation of generative linguistics. English declarative sentences are presented to the agent by a teacher in form of utterance meaning pairs (UMP) where the meanings are encoded as formulas of predicate logic. Since MG codifies universal linguistic competence through inference rules, thereby separating innate linguistic knowledge from the contingently acquired lexicon, our approach unifies generative grammar and reinforcement learning, hence potentially resolving the still pending Chomsky-Skinner controversy.

Vector symbolic architectures for context-free grammars

Background / introduction. Vector symbolic architectures (VSA) are a viable approach for the hyperdimensional representation of symbolic data, such as documents, syntactic structures, or semantic frames. Methods. We present a rigorous mathematical framework for the representation of phrase structure trees and parse-trees of context-free grammars (CFG) in Fock space, i.e. infinite-dimensional Hilbert space as being used in quantum field theory. We define a novel normal form for CFG by means of term algebras. Using a recently developed software toolbox, called FockBox, we construct Fock space representations for the trees built up by a CFG left-corner (LC) parser. Results. We prove a universal representation theorem for CFG term algebras in Fock space and illustrate our findings through a low-dimensional principal component projection of the LC parser states. Conclusions. Our approach could leverage the development of VSA for explainable artificial intelligence (XAI) by means of hyperdimensional deep neural computation. It could be of significance for the improvement of cognitive user interfaces and other applications of VSA in machine learning.

Reinforcement Learning of Minimalist Numeral Grammars

Speech-controlled user interfaces facilitate the operation of devices and household functions to laymen. State-of-the-art language technology scans the acoustically analyzed speech signal for relevant keywords that are subsequently inserted into semantic slots to interpret the user's intent. In order to develop proper cognitive information and communication technologies, simple slot-filling should be replaced by utterance meaning transducers (UMT) that are based on semantic parsers and a \emph{mental lexicon}, comprising syntactic, phonetic and semantic features of the language under consideration. This lexicon must be acquired by a cognitive agent during interaction with its users. We outline a reinforcement learning algorithm for the acquisition of the syntactic morphology and arithmetic semantics of English numerals, based on minimalist grammar (MG), a recent computational implementation of generative linguistics. Number words are presented to the agent by a teacher in form of utterance meaning pairs (UMP) where the meanings are encoded as arithmetic terms from a suitable term algebra. Since MG encodes universal linguistic competence through inference rules, thereby separating innate linguistic knowledge from the contingently acquired lexicon, our approach unifies generative grammar and reinforcement learning, hence potentially resolving the still pending Chomsky-Skinner controversy.

A modular architecture for transparent computation in Recurrent Neural Networks

Computation is classically studied in terms of automata, formal languages and algorithms; yet, the relation between neural dynamics and symbolic representations and operations is still unclear in traditional eliminative connectionism. Therefore, we suggest a unique perspective on this central issue, to which we would like to refer as to transparent connectionism, by proposing accounts of how symbolic computation can be implemented in neural substrates. In this study we first introduce a new model of dynamics on a symbolic space, the versatile shift, showing that it supports the real-time simulation of a range of automata. We then show that the Goedelization of versatile shifts defines nonlinear dynamical automata, dynamical systems evolving on a vectorial space. Finally, we present a mapping between nonlinear dynamical automata and recurrent artificial neural networks. The mapping defines an architecture characterized by its granular modularity, where data, symbolic operations and their control are not only distinguishable in activation space, but also spatially localizable in the network itself, while maintaining a distributed encoding of symbolic representations. The resulting networks simulate automata in real-time and are programmed directly, in absence of network training. To discuss the unique characteristics of the architecture and their consequences, we present two examples: i) the design of a Central Pattern Generator from a finite-state locomotive controller, and ii) the creation of a network simulating a system of interactive automata that supports the parsing of garden-path sentences as investigated in psycholinguistics experiments.

Turing Computation with Recurrent Artificial Neural Networks

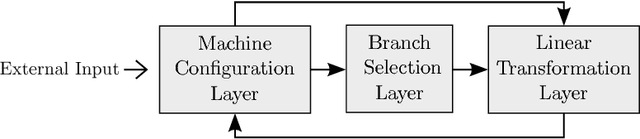
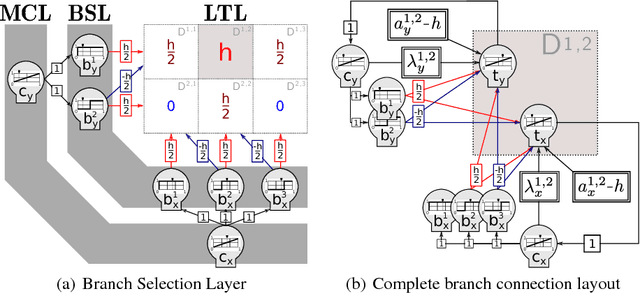
We improve the results by Siegelmann & Sontag (1995) by providing a novel and parsimonious constructive mapping between Turing Machines and Recurrent Artificial Neural Networks, based on recent developments of Nonlinear Dynamical Automata. The architecture of the resulting R-ANNs is simple and elegant, stemming from its transparent relation with the underlying NDAs. These characteristics yield promise for developments in machine learning methods and symbolic computation with continuous time dynamical systems. A framework is provided to directly program the R-ANNs from Turing Machine descriptions, in absence of network training. At the same time, the network can potentially be trained to perform algorithmic tasks, with exciting possibilities in the integration of approaches akin to Google DeepMind's Neural Turing Machines.

The Horse Raced Past: Gardenpath Processing in Dynamical Systems

I pinpoint an interesting similarity between a recent account to rational parsing and the treatment of sequential decisions problems in a dynamical systems approach. I argue that expectation-driven search heuristics aiming at fast computation resembles a high-risk decision strategy in favor of large transition velocities. Hale's rational parser, combining generalized left-corner parsing with informed $\mathrm{A}^*$ search to resolve processing conflicts, explains gardenpath effects in natural sentence processing by misleading estimates of future processing costs that are to be minimized. On the other hand, minimizing the duration of cognitive computations in time-continuous dynamical systems can be described by combining vector space representations of cognitive states by means of filler/role decompositions and subsequent tensor product representations with the paradigm of stable heteroclinic sequences. Maximizing transition velocities according to a high-risk decision strategy could account for a fast race even between states that are apparently remote in representation space.

Geometric representations for minimalist grammars

We reformulate minimalist grammars as partial functions on term algebras for strings and trees. Using filler/role bindings and tensor product representations, we construct homomorphisms for these data structures into geometric vector spaces. We prove that the structure-building functions as well as simple processors for minimalist languages can be realized by piecewise linear operators in representation space. We also propose harmony, i.e. the distance of an intermediate processing step from the final well-formed state in representation space, as a measure of processing complexity. Finally, we illustrate our findings by means of two particular arithmetic and fractal representations.