A Principled Method for the Creation of Synthetic Multi-fidelity Data Sets

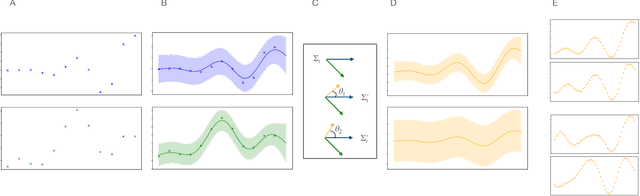
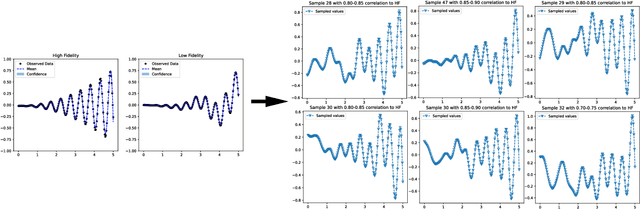
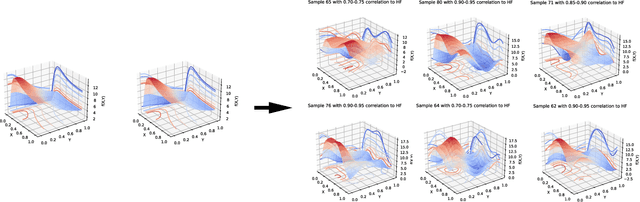
Multifidelity and multioutput optimisation algorithms are of active interest in many areas of computational design as they allow cheaper computational proxies to be used intelligently to aid experimental searches for high-performing species. Characterisation of these algorithms involves benchmarks that typically either use analytic functions or existing multifidelity datasets. However, analytic functions are often not representative of relevant problems, while preexisting datasets do not allow systematic investigation of the influence of characteristics of the lower fidelity proxies. To bridge this gap, we present a methodology for systematic generation of synthetic fidelities derived from preexisting datasets. This allows for the construction of benchmarks that are both representative of practical optimisation problems while also allowing systematic investigation of the influence of the lower fidelity proxies.

Privacy-Preserving Gaussian Process Regression -- A Modular Approach to the Application of Homomorphic Encryption

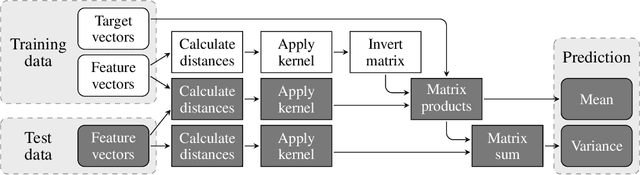
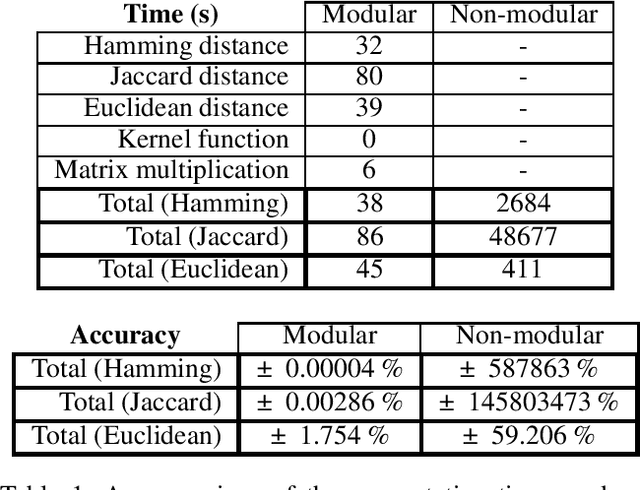
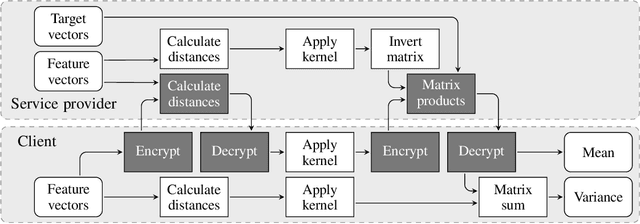
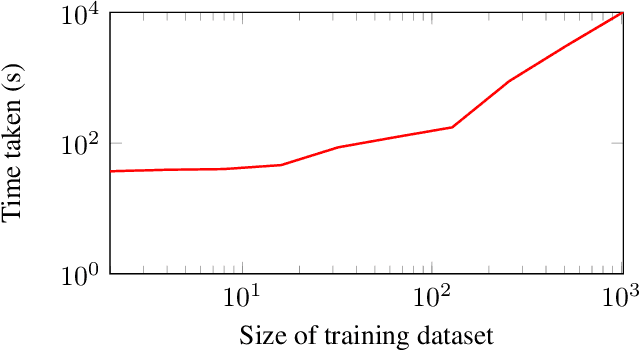
Much of machine learning relies on the use of large amounts of data to train models to make predictions. When this data comes from multiple sources, for example when evaluation of data against a machine learning model is offered as a service, there can be privacy issues and legal concerns over the sharing of data. Fully homomorphic encryption (FHE) allows data to be computed on whilst encrypted, which can provide a solution to the problem of data privacy. However, FHE is both slow and restrictive, so existing algorithms must be manipulated to make them work efficiently under the FHE paradigm. Some commonly used machine learning algorithms, such as Gaussian process regression, are poorly suited to FHE and cannot be manipulated to work both efficiently and accurately. In this paper, we show that a modular approach, which applies FHE to only the sensitive steps of a workflow that need protection, allows one party to make predictions on their data using a Gaussian process regression model built from another party's data, without either party gaining access to the other's data, in a way which is both accurate and efficient. This construction is, to our knowledge, the first example of an effectively encrypted Gaussian process.