Privacy-Preserving Gaussian Process Regression -- A Modular Approach to the Application of Homomorphic Encryption
Paper and Code
Jan 28, 2020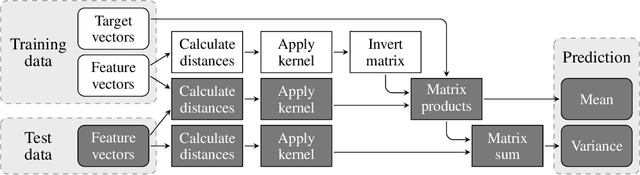
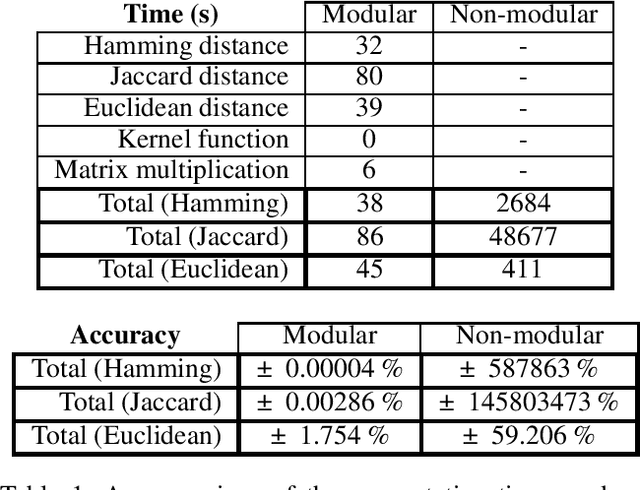
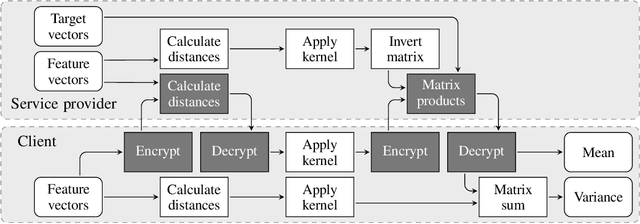
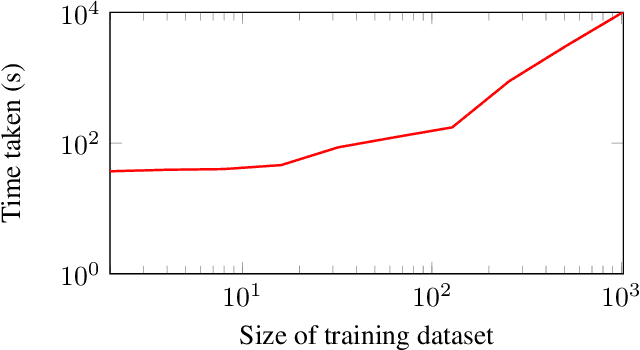
Much of machine learning relies on the use of large amounts of data to train models to make predictions. When this data comes from multiple sources, for example when evaluation of data against a machine learning model is offered as a service, there can be privacy issues and legal concerns over the sharing of data. Fully homomorphic encryption (FHE) allows data to be computed on whilst encrypted, which can provide a solution to the problem of data privacy. However, FHE is both slow and restrictive, so existing algorithms must be manipulated to make them work efficiently under the FHE paradigm. Some commonly used machine learning algorithms, such as Gaussian process regression, are poorly suited to FHE and cannot be manipulated to work both efficiently and accurately. In this paper, we show that a modular approach, which applies FHE to only the sensitive steps of a workflow that need protection, allows one party to make predictions on their data using a Gaussian process regression model built from another party's data, without either party gaining access to the other's data, in a way which is both accurate and efficient. This construction is, to our knowledge, the first example of an effectively encrypted Gaussian process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge