Evolution of Hierarchical Structure & Reuse in iGEM Synthetic DNA Sequences

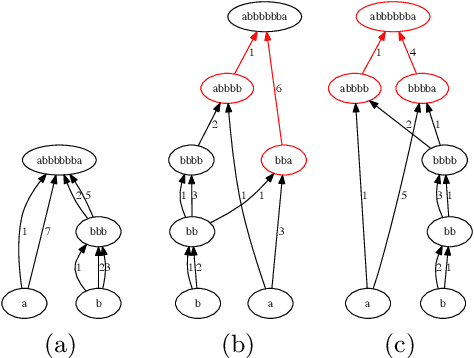
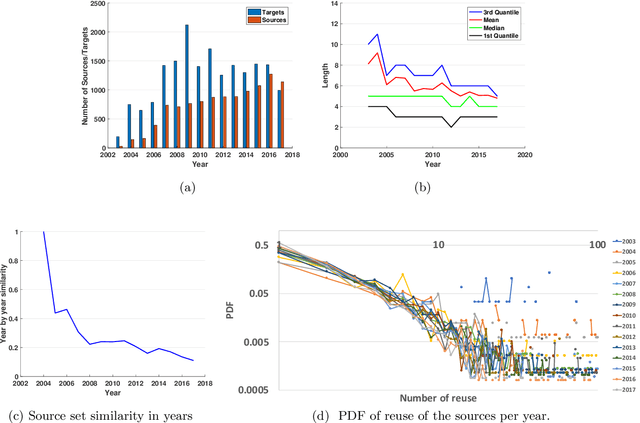
Many complex systems, both in technology and nature, exhibit hierarchical modularity: smaller modules, each of them providing a certain function, are used within larger modules that perform more complex functions. Previously, we have proposed a modeling framework, referred to as Evo-Lexis, that provides insight to some fundamental questions about evolving hierarchical systems. The predictions of the Evo-Lexis model should be tested using real data from evolving systems in which the outputs can be well represented by sequences. In this paper, we investigate the time series of iGEM synthetic DNA dataset sequences, and whether the resulting iGEM hierarchies exhibit the qualitative properties predicted by the Evo-Lexis framework. Contrary to Evo-Lexis, in iGEM the amount of reuse decreases during the timeline of the dataset. Although this results in development of less cost-efficient and less deep Lexis-DAGs, the dataset exhibits a bias in reusing specific nodes more often than others. This results in the Lexis-DAGs to take the shape of an hourglass with relatively high H-score values and stable set of core nodes. Despite the reuse bias and stability of the core set, the dataset presents a high amount of diversity among the targets which is in line with modeling of Evo-Lexis.

Emergence and Evolution of Hierarchical Structure in Complex Systems

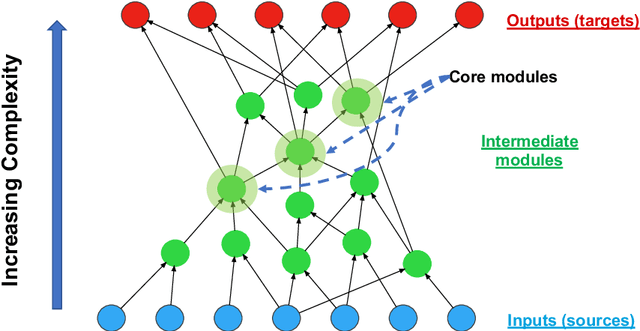
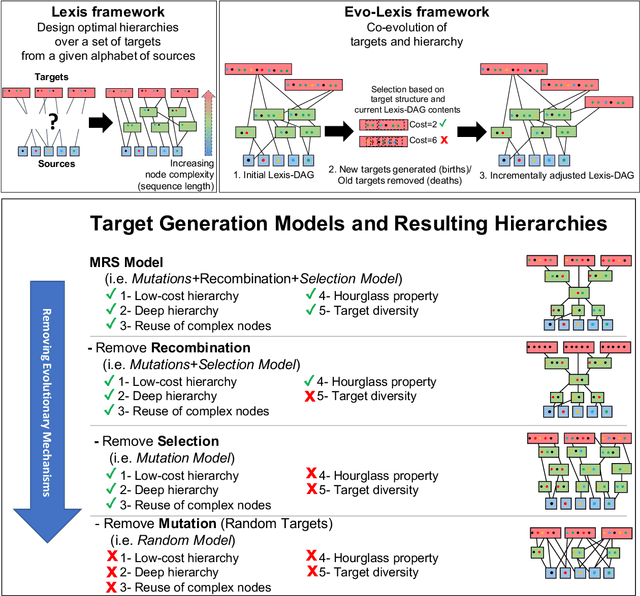
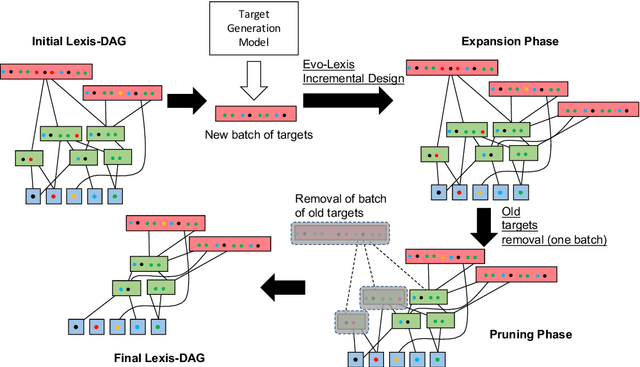
It is well known that many complex systems, both in technology and nature, exhibit hierarchical modularity: smaller modules, each of them providing a certain function, are used within larger modules that perform more complex functions. What is not well understood however is how this hierarchical structure (which is fundamentally a network property) emerges, and how it evolves over time. We propose a modeling framework, referred to as Evo-Lexis, that provides insight to some fundamental questions about evolving hierarchical systems. Evo-Lexis models the most elementary modules of the system as symbols ("sources") and the modules at the highest level of the hierarchy as sequences of those symbols ("targets"). Evo-Lexis computes the optimized adjustment of a given hierarchy when the set of targets changes over time by additions and removals (a process referred to as "incremental design"). In this paper we use computation modeling to show that: - Low-cost and deep hierarchies emerge when the population of target sequences evolves through tinkering and mutation. - Strong selection on the cost of new candidate targets results in reuse of more complex (longer) nodes in an optimized hierarchy. - The bias towards reuse of complex nodes results in an "hourglass architecture" (i.e., few intermediate nodes that cover almost all source-target paths). - With such bias, the core nodes are conserved for relatively long time periods although still being vulnerable to major transitions and punctuated equilibria. - Finally, we analyze the differences in terms of cost and structure between incrementally designed hierarchies and the corresponding "clean-slate" hierarchies which result when the system is designed from scratch after a change.

The Generalized Smallest Grammar Problem

The Smallest Grammar Problem -- the problem of finding the smallest context-free grammar that generates exactly one given sequence -- has never been successfully applied to grammatical inference. We investigate the reasons and propose an extended formulation that seeks to minimize non-recursive grammars, instead of straight-line programs. In addition, we provide very efficient algorithms that approximate the minimization problem of this class of grammars. Our empirical evaluation shows that we are able to find smaller models than the current best approximations to the Smallest Grammar Problem on standard benchmarks, and that the inferred rules capture much better the syntactic structure of natural language.

Lexis: An Optimization Framework for Discovering the Hierarchical Structure of Sequential Data

Data represented as strings abounds in biology, linguistics, document mining, web search and many other fields. Such data often have a hierarchical structure, either because they were artificially designed and composed in a hierarchical manner or because there is an underlying evolutionary process that creates repeatedly more complex strings from simpler substrings. We propose a framework, referred to as "Lexis", that produces an optimized hierarchical representation of a given set of "target" strings. The resulting hierarchy, "Lexis-DAG", shows how to construct each target through the concatenation of intermediate substrings, minimizing the total number of such concatenations or DAG edges. The Lexis optimization problem is related to the smallest grammar problem. After we prove its NP-Hardness for two cost formulations, we propose an efficient greedy algorithm for the construction of Lexis-DAGs. We also consider the problem of identifying the set of intermediate nodes (substrings) that collectively form the "core" of a Lexis-DAG, which is important in the analysis of Lexis-DAGs. We show that the Lexis framework can be applied in diverse applications such as optimized synthesis of DNA fragments in genomic libraries, hierarchical structure discovery in protein sequences, dictionary-based text compression, and feature extraction from a set of documents.