Generalization Properties of Adversarial Training for $\ell_0$-Bounded Adversarial Attacks

We have widely observed that neural networks are vulnerable to small additive perturbations to the input causing misclassification. In this paper, we focus on the $\ell_0$-bounded adversarial attacks, and aim to theoretically characterize the performance of adversarial training for an important class of truncated classifiers. Such classifiers are shown to have strong performance empirically, as well as theoretically in the Gaussian mixture model, in the $\ell_0$-adversarial setting. The main contribution of this paper is to prove a novel generalization bound for the binary classification setting with $\ell_0$-bounded adversarial perturbation that is distribution-independent. Deriving a generalization bound in this setting has two main challenges: (i) the truncated inner product which is highly non-linear; and (ii) maximization over the $\ell_0$ ball due to adversarial training is non-convex and highly non-smooth. To tackle these challenges, we develop new coding techniques for bounding the combinatorial dimension of the truncated hypothesis class.

Binary Classification Under $\ell_0$ Attacks for General Noise Distribution

Adversarial examples have recently drawn considerable attention in the field of machine learning due to the fact that small perturbations in the data can result in major performance degradation. This phenomenon is usually modeled by a malicious adversary that can apply perturbations to the data in a constrained fashion, such as being bounded in a certain norm. In this paper, we study this problem when the adversary is constrained by the $\ell_0$ norm; i.e., it can perturb a certain number of coordinates in the input, but has no limit on how much it can perturb those coordinates. Due to the combinatorial nature of this setting, we need to go beyond the standard techniques in robust machine learning to address this problem. We consider a binary classification scenario where $d$ noisy data samples of the true label are provided to us after adversarial perturbations. We introduce a classification method which employs a nonlinear component called truncation, and show in an asymptotic scenario, as long as the adversary is restricted to perturb no more than $\sqrt{d}$ data samples, we can almost achieve the optimal classification error in the absence of the adversary, i.e. we can completely neutralize adversary's effect. Surprisingly, we observe a phase transition in the sense that using a converse argument, we show that if the adversary can perturb more than $\sqrt{d}$ coordinates, no classifier can do better than a random guess.

Efficient and Robust Classification for Sparse Attacks

In the past two decades we have seen the popularity of neural networks increase in conjunction with their classification accuracy. Parallel to this, we have also witnessed how fragile the very same prediction models are: tiny perturbations to the inputs can cause misclassification errors throughout entire datasets. In this paper, we consider perturbations bounded by the $\ell_0$--norm, which have been shown as effective attacks in the domains of image-recognition, natural language processing, and malware-detection. To this end, we propose a novel defense method that consists of "truncation" and "adversarial training". We then theoretically study the Gaussian mixture setting and prove the asymptotic optimality of our proposed classifier. Motivated by the insights we obtain, we extend these components to neural network classifiers. We conduct numerical experiments in the domain of computer vision using the MNIST and CIFAR datasets, demonstrating significant improvement for the robust classification error of neural networks.

Robust Classification Under $\ell_0$ Attack for the Gaussian Mixture Model

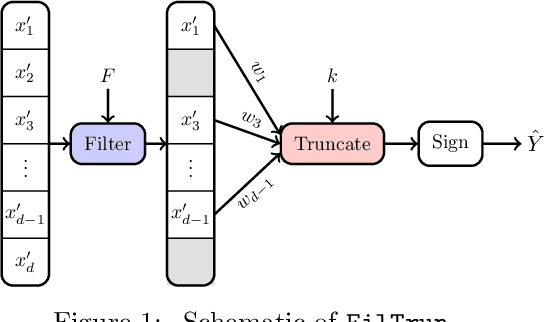
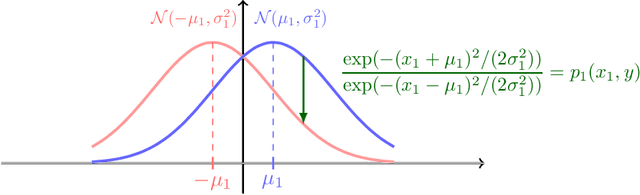
It is well-known that machine learning models are vulnerable to small but cleverly-designed adversarial perturbations that can cause misclassification. While there has been major progress in designing attacks and defenses for various adversarial settings, many fundamental and theoretical problems are yet to be resolved. In this paper, we consider classification in the presence of $\ell_0$-bounded adversarial perturbations, a.k.a. sparse attacks. This setting is significantly different from other $\ell_p$-adversarial settings, with $p\geq 1$, as the $\ell_0$-ball is non-convex and highly non-smooth. Under the assumption that data is distributed according to the Gaussian mixture model, our goal is to characterize the optimal robust classifier and the corresponding robust classification error as well as a variety of trade-offs between robustness, accuracy, and the adversary's budget. To this end, we develop a novel classification algorithm called FilTrun that has two main modules: Filtration and Truncation. The key idea of our method is to first filter out the non-robust coordinates of the input and then apply a carefully-designed truncated inner product for classification. By analyzing the performance of FilTrun, we derive an upper bound on the optimal robust classification error. We also find a lower bound by designing a specific adversarial strategy that enables us to derive the corresponding robust classifier and its achieved error. For the case that the covariance matrix of the Gaussian mixtures is diagonal, we show that as the input's dimension gets large, the upper and lower bounds converge; i.e. we characterize the asymptotically-optimal robust classifier. Throughout, we discuss several examples that illustrate interesting behaviors such as the existence of a phase transition for adversary's budget determining whether the effect of adversarial perturbation can be fully neutralized.

Deep Switch Networks for Generating Discrete Data and Language

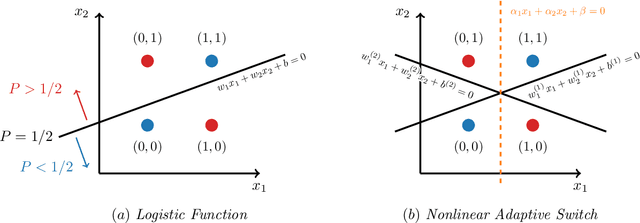
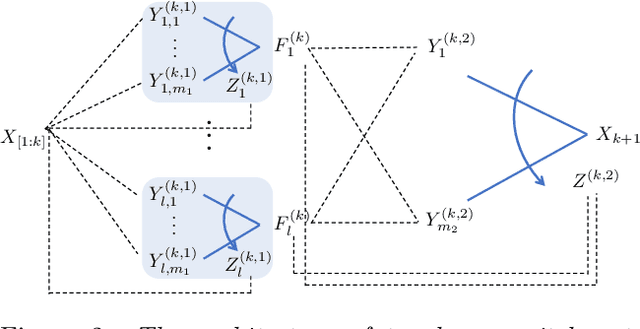
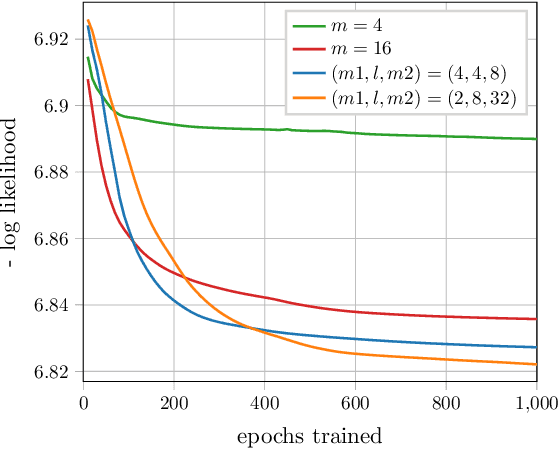
Multilayer switch networks are proposed as artificial generators of high-dimensional discrete data (e.g., binary vectors, categorical data, natural language, network log files, and discrete-valued time series). Unlike deconvolution networks which generate continuous-valued data and which consist of upsampling filters and reverse pooling layers, multilayer switch networks are composed of adaptive switches which model conditional distributions of discrete random variables. An interpretable, statistical framework is introduced for training these nonlinear networks based on a maximum-likelihood objective function. To learn network parameters, stochastic gradient descent is applied to the objective. This direct optimization is stable until convergence, and does not involve back-propagation over separate encoder and decoder networks, or adversarial training of dueling networks. While training remains tractable for moderately sized networks, Markov-chain Monte Carlo (MCMC) approximations of gradients are derived for deep networks which contain latent variables. The statistical framework is evaluated on synthetic data, high-dimensional binary data of handwritten digits, and web-crawled natural language data. Aspects of the model's framework such as interpretability, computational complexity, and generalization ability are discussed.