Sail into the Headwind: Alignment via Robust Rewards and Dynamic Labels against Reward Hacking

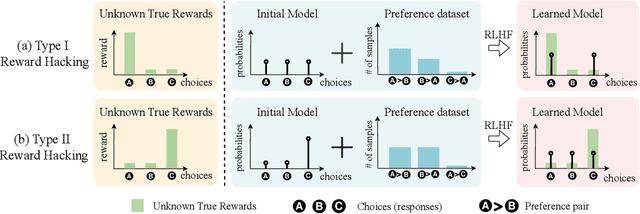
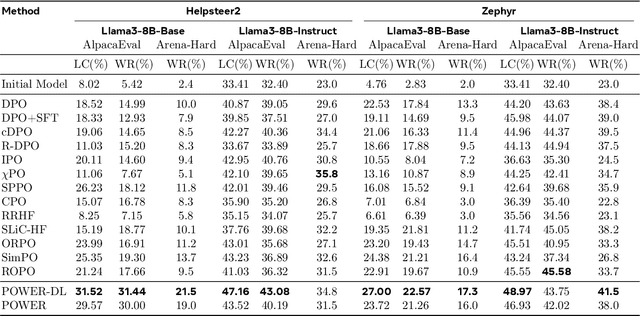
Aligning AI systems with human preferences typically suffers from the infamous reward hacking problem, where optimization of an imperfect reward model leads to undesired behaviors. In this paper, we investigate reward hacking in offline preference optimization, which aims to improve an initial model using a preference dataset. We identify two types of reward hacking stemming from statistical fluctuations in the dataset: Type I Reward Hacking due to subpar choices appearing more favorable, and Type II Reward Hacking due to decent choices appearing less favorable. We prove that many (mainstream or theoretical) preference optimization methods suffer from both types of reward hacking. To mitigate Type I Reward Hacking, we propose POWER, a new preference optimization method that combines Guiasu's weighted entropy with a robust reward maximization objective. POWER enjoys finite-sample guarantees under general function approximation, competing with the best covered policy in the data. To mitigate Type II Reward Hacking, we analyze the learning dynamics of preference optimization and develop a novel technique that dynamically updates preference labels toward certain "stationary labels", resulting in diminishing gradients for untrustworthy samples. Empirically, POWER with dynamic labels (POWER-DL) consistently outperforms state-of-the-art methods on alignment benchmarks, achieving improvements of up to 13.0 points on AlpacaEval 2.0 and 11.5 points on Arena-Hard over DPO, while also improving or maintaining performance on downstream tasks such as mathematical reasoning. Strong theoretical guarantees and empirical results demonstrate the promise of POWER-DL in mitigating reward hacking.

Importance Weighted Actor-Critic for Optimal Conservative Offline Reinforcement Learning

We propose A-Crab (Actor-Critic Regularized by Average Bellman error), a new algorithm for offline reinforcement learning (RL) in complex environments with insufficient data coverage. Our algorithm combines the marginalized importance sampling framework with the actor-critic paradigm, where the critic returns evaluations of the actor (policy) that are pessimistic relative to the offline data and have a small average (importance-weighted) Bellman error. Compared to existing methods, our algorithm simultaneously offers a number of advantages: (1) It is practical and achieves the optimal statistical rate of $1/\sqrt{N}$ -- where $N$ is the size of the offline dataset -- in converging to the best policy covered in the offline dataset, even when combined with general function approximations. (2) It relies on a weaker average notion of policy coverage (compared to the $\ell_\infty$ single-policy concentrability) that exploits the structure of policy visitations. (3) It outperforms the data-collection behavior policy over a wide-range of hyperparameters and is the first algorithm to do so without solving a minimax optimization problem.

Optimal Conservative Offline RL with General Function Approximation via Augmented Lagrangian

Offline reinforcement learning (RL), which refers to decision-making from a previously-collected dataset of interactions, has received significant attention over the past years. Much effort has focused on improving offline RL practicality by addressing the prevalent issue of partial data coverage through various forms of conservative policy learning. While the majority of algorithms do not have finite-sample guarantees, several provable conservative offline RL algorithms are designed and analyzed within the single-policy concentrability framework that handles partial coverage. Yet, in the nonlinear function approximation setting where confidence intervals are difficult to obtain, existing provable algorithms suffer from computational intractability, prohibitively strong assumptions, and suboptimal statistical rates. In this paper, we leverage the marginalized importance sampling (MIS) formulation of RL and present the first set of offline RL algorithms that are statistically optimal and practical under general function approximation and single-policy concentrability, bypassing the need for uncertainty quantification. We identify that the key to successfully solving the sample-based approximation of the MIS problem is ensuring that certain occupancy validity constraints are nearly satisfied. We enforce these constraints by a novel application of the augmented Lagrangian method and prove the following result: with the MIS formulation, augmented Lagrangian is enough for statistically optimal offline RL. In stark contrast to prior algorithms that induce additional conservatism through methods such as behavior regularization, our approach provably eliminates this need and reinterprets regularizers as "enforcers of occupancy validity" than "promoters of conservatism."

MADE: Exploration via Maximizing Deviation from Explored Regions

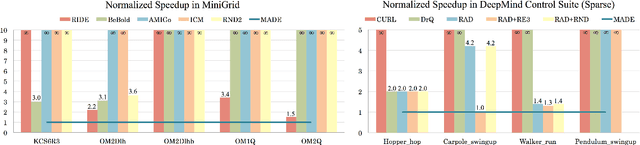
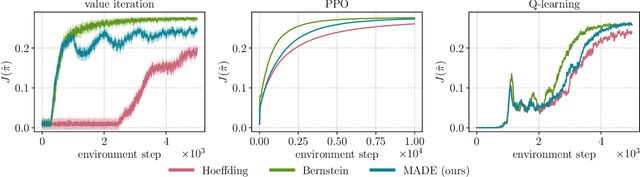
In online reinforcement learning (RL), efficient exploration remains particularly challenging in high-dimensional environments with sparse rewards. In low-dimensional environments, where tabular parameterization is possible, count-based upper confidence bound (UCB) exploration methods achieve minimax near-optimal rates. However, it remains unclear how to efficiently implement UCB in realistic RL tasks that involve non-linear function approximation. To address this, we propose a new exploration approach via \textit{maximizing} the deviation of the occupancy of the next policy from the explored regions. We add this term as an adaptive regularizer to the standard RL objective to balance exploration vs. exploitation. We pair the new objective with a provably convergent algorithm, giving rise to a new intrinsic reward that adjusts existing bonuses. The proposed intrinsic reward is easy to implement and combine with other existing RL algorithms to conduct exploration. As a proof of concept, we evaluate the new intrinsic reward on tabular examples across a variety of model-based and model-free algorithms, showing improvements over count-only exploration strategies. When tested on navigation and locomotion tasks from MiniGrid and DeepMind Control Suite benchmarks, our approach significantly improves sample efficiency over state-of-the-art methods. Our code is available at https://github.com/tianjunz/MADE.

Bridging Offline Reinforcement Learning and Imitation Learning: A Tale of Pessimism

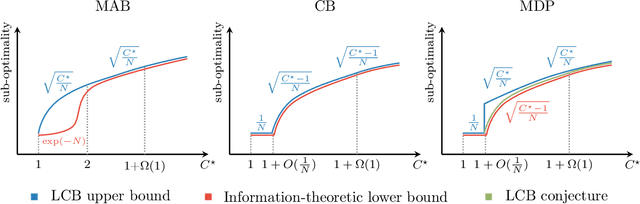
Offline (or batch) reinforcement learning (RL) algorithms seek to learn an optimal policy from a fixed dataset without active data collection. Based on the composition of the offline dataset, two main categories of methods are used: imitation learning which is suitable for expert datasets and vanilla offline RL which often requires uniform coverage datasets. From a practical standpoint, datasets often deviate from these two extremes and the exact data composition is usually unknown a priori. To bridge this gap, we present a new offline RL framework that smoothly interpolates between the two extremes of data composition, hence unifying imitation learning and vanilla offline RL. The new framework is centered around a weak version of the concentrability coefficient that measures the deviation from the behavior policy to the expert policy alone. Under this new framework, we further investigate the question on algorithm design: can one develop an algorithm that achieves a minimax optimal rate and also adapts to unknown data composition? To address this question, we consider a lower confidence bound (LCB) algorithm developed based on pessimism in the face of uncertainty in offline RL. We study finite-sample properties of LCB as well as information-theoretic limits in multi-armed bandits, contextual bandits, and Markov decision processes (MDPs). Our analysis reveals surprising facts about optimality rates. In particular, in all three settings, LCB achieves a faster rate of $1/N$ for nearly-expert datasets compared to the usual rate of $1/\sqrt{N}$ in offline RL, where $N$ is the number of samples in the batch dataset. In the case of contextual bandits with at least two contexts, we prove that LCB is adaptively optimal for the entire data composition range, achieving a smooth transition from imitation learning to offline RL. We further show that LCB is almost adaptively optimal in MDPs.

SLIP: Learning to Predict in Unknown Dynamical Systems with Long-Term Memory

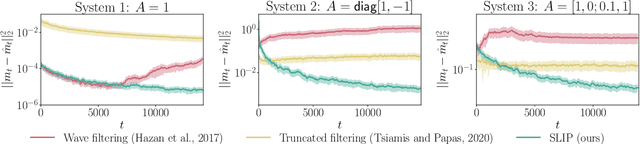
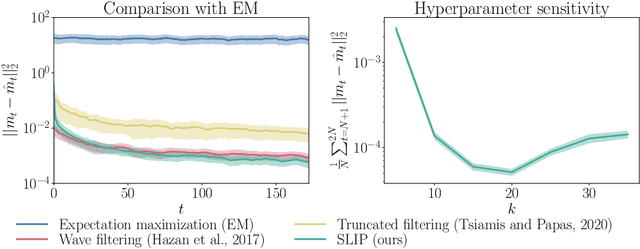
We present an efficient and practical (polynomial time) algorithm for online prediction in unknown and partially observed linear dynamical systems (LDS) under stochastic noise. When the system parameters are known, the optimal linear predictor is the Kalman filter. However, the performance of existing predictive models is poor in important classes of LDS that are only marginally stable and exhibit long-term forecast memory. We tackle this problem through bounding the generalized Kolmogorov width of the Kalman filter model by spectral methods and conducting tight convex relaxation. We provide a finite-sample analysis, showing that our algorithm competes with Kalman filter in hindsight with only logarithmic regret. Our regret analysis relies on Mendelson's small-ball method, providing sharp error bounds without concentration, boundedness, or exponential forgetting assumptions. We also give experimental results demonstrating that our algorithm outperforms state-of-the-art methods. Our theoretical and experimental results shed light on the conditions required for efficient probably approximately correct (PAC) learning of the Kalman filter from partially observed data.