Improving Explainability of Disentangled Representations using Multipath-Attribution Mappings

Explainable AI aims to render model behavior understandable by humans, which can be seen as an intermediate step in extracting causal relations from correlative patterns. Due to the high risk of possible fatal decisions in image-based clinical diagnostics, it is necessary to integrate explainable AI into these safety-critical systems. Current explanatory methods typically assign attribution scores to pixel regions in the input image, indicating their importance for a model's decision. However, they fall short when explaining why a visual feature is used. We propose a framework that utilizes interpretable disentangled representations for downstream-task prediction. Through visualizing the disentangled representations, we enable experts to investigate possible causation effects by leveraging their domain knowledge. Additionally, we deploy a multi-path attribution mapping for enriching and validating explanations. We demonstrate the effectiveness of our approach on a synthetic benchmark suite and two medical datasets. We show that the framework not only acts as a catalyst for causal relation extraction but also enhances model robustness by enabling shortcut detection without the need for testing under distribution shifts.

On maximum-likelihood estimation in the all-or-nothing regime

We study the problem of estimating a rank-1 additive deformation of a Gaussian tensor according to the \emph{maximum-likelihood estimator} (MLE). The analysis is carried out in the sparse setting, where the underlying signal has a support that scales sublinearly with the total number of dimensions. We show that for Bernoulli distributed signals, the MLE undergoes an \emph{all-or-nothing} (AoN) phase transition, already established for the minimum mean-square-error estimator (MMSE) in the same problem. The result follows from two main technical points: (i) the connection established between the MLE and the MMSE, using the first and second-moment methods in the constrained signal space, (ii) a recovery regime for the MMSE stricter than the simple error vanishing characterization given in the standard AoN, that is here proved as a general result.

Statistical and computational thresholds for the planted $k$-densest sub-hypergraph problem

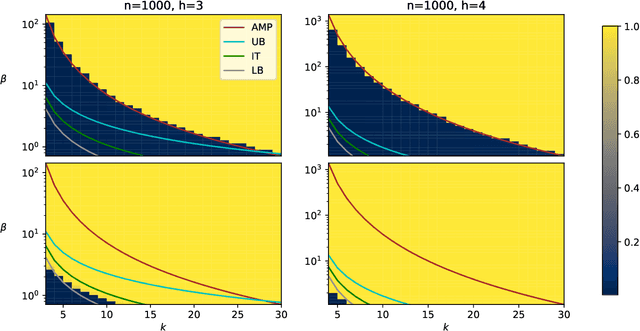
Recovery a planted signal perturbed by noise is a fundamental problem in machine learning. In this work, we consider the problem of recovery a planted $k$-densest sub-hypergraph on $h$-uniform hypergraphs over $n$ nodes. This fundamental problem appears in different contexts, e.g., community detection, average case complexity, and neuroscience applications. We first observe that it can be viewed as a structural variant of tensor PCA in which the hypergraph parameters $k$ and $h$ determine the structure of the signal to be recovered when the observations are contaminated by Gaussian noise. In this work, we provide tight information-theoretic upper and lower bounds for the recovery problem, as well as the first non-trivial algorithmic bounds based on approximate message passing algorithms. The problem exhibits a typical information-to-computational-gap observed in analogous settings, that widens with increasing sparsity of the problem. Interestingly, the bounds show that the structure of the signal does have an impact on the existing bounds of tensor PCA that the unstructured planted signal does not capture.