Statistical and computational thresholds for the planted $k$-densest sub-hypergraph problem
Paper and Code
Nov 23, 2020

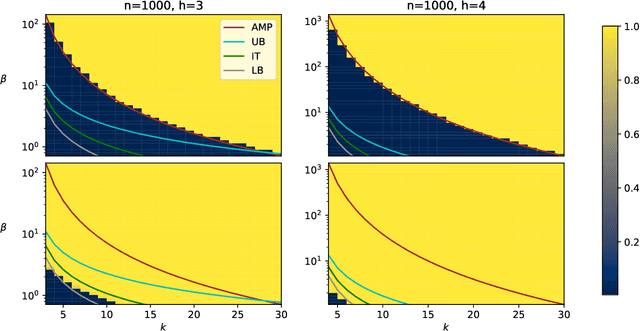
Recovery a planted signal perturbed by noise is a fundamental problem in machine learning. In this work, we consider the problem of recovery a planted $k$-densest sub-hypergraph on $h$-uniform hypergraphs over $n$ nodes. This fundamental problem appears in different contexts, e.g., community detection, average case complexity, and neuroscience applications. We first observe that it can be viewed as a structural variant of tensor PCA in which the hypergraph parameters $k$ and $h$ determine the structure of the signal to be recovered when the observations are contaminated by Gaussian noise. In this work, we provide tight information-theoretic upper and lower bounds for the recovery problem, as well as the first non-trivial algorithmic bounds based on approximate message passing algorithms. The problem exhibits a typical information-to-computational-gap observed in analogous settings, that widens with increasing sparsity of the problem. Interestingly, the bounds show that the structure of the signal does have an impact on the existing bounds of tensor PCA that the unstructured planted signal does not capture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge