Community Detection and Classification Guarantees Using Embeddings Learned by Node2Vec

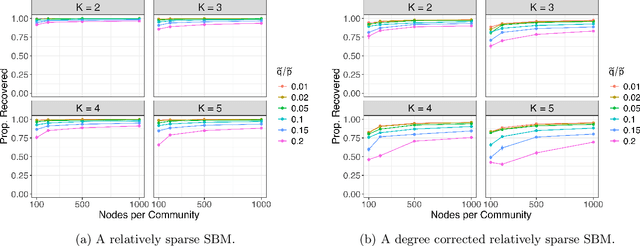
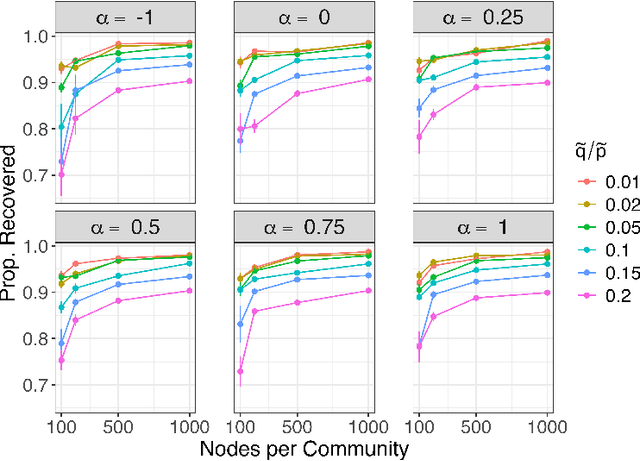
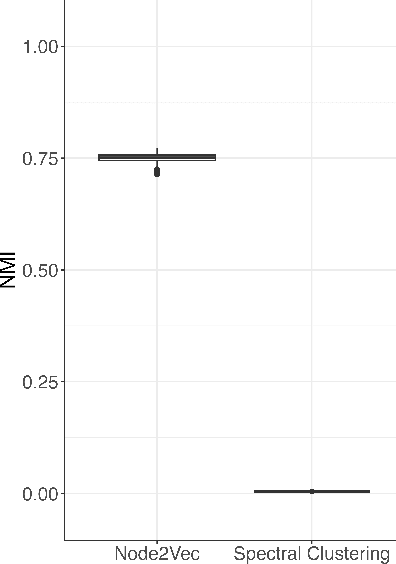
Embedding the nodes of a large network into an Euclidean space is a common objective in modern machine learning, with a variety of tools available. These embeddings can then be used as features for tasks such as community detection/node clustering or link prediction, where they achieve state of the art performance. With the exception of spectral clustering methods, there is little theoretical understanding for other commonly used approaches to learning embeddings. In this work we examine the theoretical properties of the embeddings learned by node2vec. Our main result shows that the use of k-means clustering on the embedding vectors produced by node2vec gives weakly consistent community recovery for the nodes in (degree corrected) stochastic block models. We also discuss the use of these embeddings for node and link prediction tasks. We demonstrate this result empirically, and examine how this relates to other embedding tools for network data.

Online Community Detection for Event Streams on Networks

A common goal in network modeling is to uncover the latent community structure present among nodes. For many real-world networks, observed connections consist of events arriving as streams, which are then aggregated to form edges, ignoring the temporal dynamic component. A natural way to take account of this temporal dynamic component of interactions is to use point processes as the foundation of the network models for community detection. Computational complexity hampers the scalability of such approaches to large sparse networks. To circumvent this challenge, we propose a fast online variational inference algorithm for learning the community structure underlying dynamic event arrivals on a network using continuous-time point process latent network models. We provide regret bounds on the loss function of this procedure, giving theoretical guarantees on performance. The proposed algorithm is illustrated, using both simulation studies and real data, to have comparable performance in terms of community structure in terms of community recovery to non-online variants. Our proposed framework can also be readily modified to incorporate other popular network structures.

Next Waves in Veridical Network Embedding

Embedding nodes of a large network into a metric (e.g., Euclidean) space has become an area of active research in statistical machine learning, which has found applications in natural and social sciences. Generally, a representation of a network object is learned in a Euclidean geometry and is then used for subsequent tasks regarding the nodes and/or edges of the network, such as community detection, node classification and link prediction. Network embedding algorithms have been proposed in multiple disciplines, often with domain-specific notations and details. In addition, different measures and tools have been adopted to evaluate and compare the methods proposed under different settings, often dependent of the downstream tasks. As a result, it is challenging to study these algorithms in the literature systematically. Motivated by the recently proposed Veridical Data Science (VDS) framework, we propose a framework for network embedding algorithms and discuss how the principles of predictability, computability and stability apply in this context. The utilization of this framework in network embedding holds the potential to motivate and point to new directions for future research.