Community Detection and Classification Guarantees Using Embeddings Learned by Node2Vec
Paper and Code
Oct 26, 2023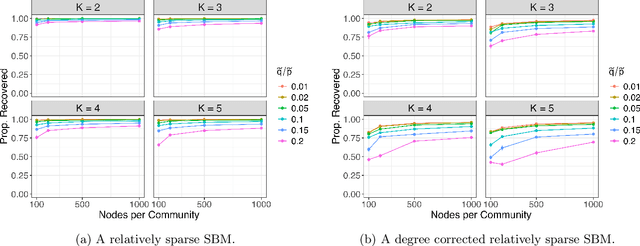
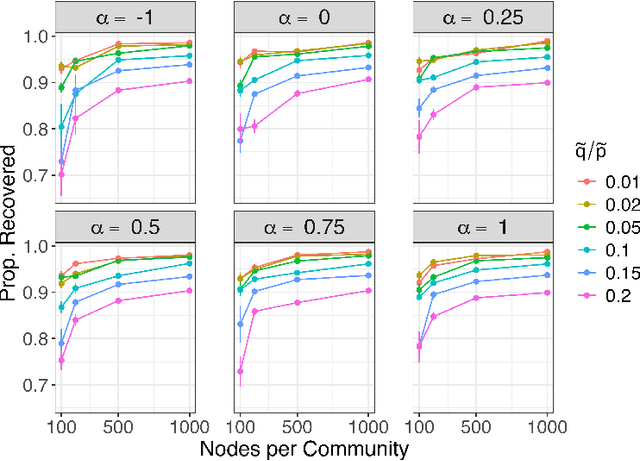
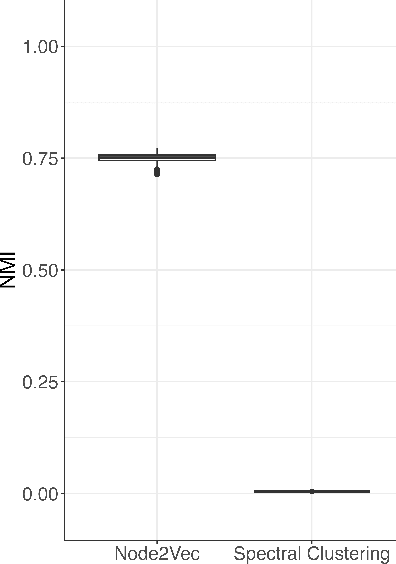
Embedding the nodes of a large network into an Euclidean space is a common objective in modern machine learning, with a variety of tools available. These embeddings can then be used as features for tasks such as community detection/node clustering or link prediction, where they achieve state of the art performance. With the exception of spectral clustering methods, there is little theoretical understanding for other commonly used approaches to learning embeddings. In this work we examine the theoretical properties of the embeddings learned by node2vec. Our main result shows that the use of k-means clustering on the embedding vectors produced by node2vec gives weakly consistent community recovery for the nodes in (degree corrected) stochastic block models. We also discuss the use of these embeddings for node and link prediction tasks. We demonstrate this result empirically, and examine how this relates to other embedding tools for network data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge