Graph Laplacian-based Bayesian Multi-fidelity Modeling

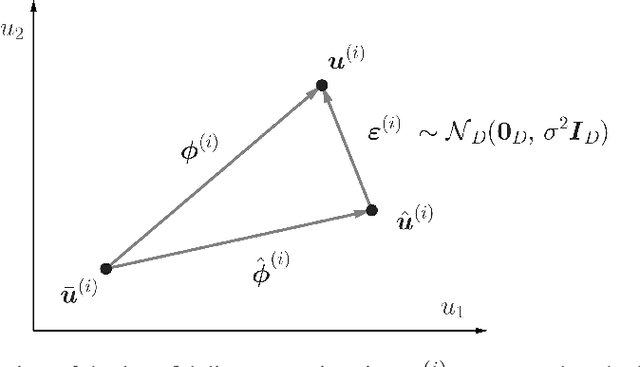
We present a novel probabilistic approach for generating multi-fidelity data while accounting for errors inherent in both low- and high-fidelity data. In this approach a graph Laplacian constructed from the low-fidelity data is used to define a multivariate Gaussian prior density for the coordinates of the true data points. In addition, few high-fidelity data points are used to construct a conjugate likelihood term. Thereafter, Bayes rule is applied to derive an explicit expression for the posterior density which is also multivariate Gaussian. The maximum \textit{a posteriori} (MAP) estimate of this density is selected to be the optimal multi-fidelity estimate. It is shown that the MAP estimate and the covariance of the posterior density can be determined through the solution of linear systems of equations. Thereafter, two methods, one based on spectral truncation and another based on a low-rank approximation, are developed to solve these equations efficiently. The multi-fidelity approach is tested on a variety of problems in solid and fluid mechanics with data that represents vectors of quantities of interest and discretized spatial fields in one and two dimensions. The results demonstrate that by utilizing a small fraction of high-fidelity data, the multi-fidelity approach can significantly improve the accuracy of a large collection of low-fidelity data points.

A few-shot graph Laplacian-based approach for improving the accuracy of low-fidelity data

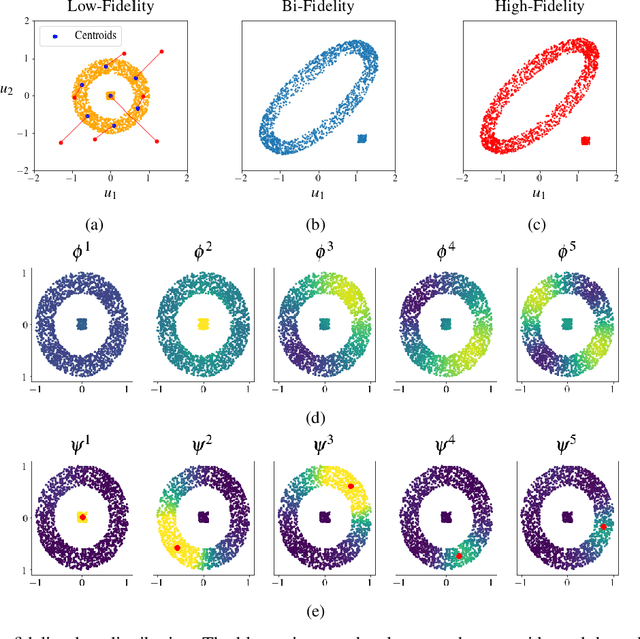
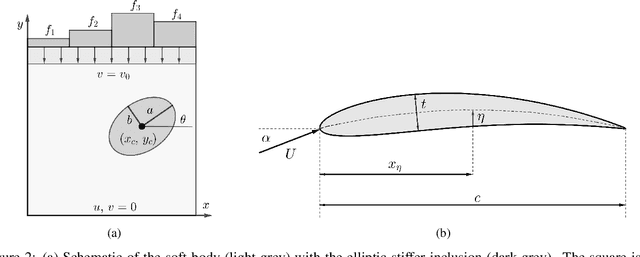
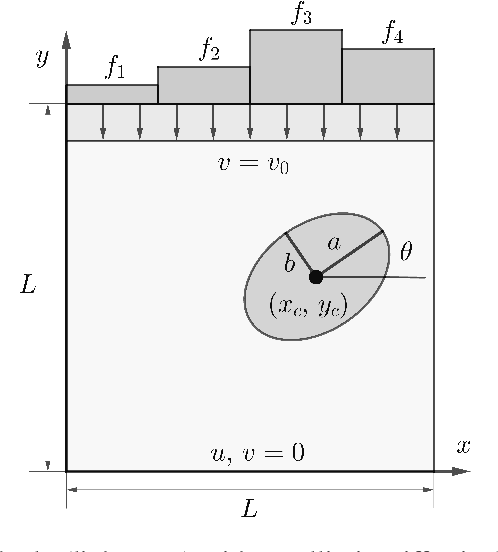
Low-fidelity data is typically inexpensive to generate but inaccurate. On the other hand, high-fidelity data is accurate but expensive to obtain. Multi-fidelity methods use a small set of high-fidelity data to enhance the accuracy of a large set of low-fidelity data. In the approach described in this paper, this is accomplished by constructing a graph Laplacian using the low-fidelity data and computing its low-lying spectrum. This spectrum is then used to cluster the data and identify points that are closest to the centroids of the clusters. High-fidelity data is then acquired for these key points. Thereafter, a transformation that maps every low-fidelity data point to its bi-fidelity counterpart is determined by minimizing the discrepancy between the bi- and high-fidelity data at the key points, and to preserve the underlying structure of the low-fidelity data distribution. The latter objective is achieved by relying, once again, on the spectral properties of the graph Laplacian. This method is applied to a problem in solid mechanics and another in aerodynamics. In both cases, this methods uses a small fraction of high-fidelity data to significantly improve the accuracy of a large set of low-fidelity data.

Deep Learning and Computational Physics (Lecture Notes)

These notes were compiled as lecture notes for a course developed and taught at the University of the Southern California. They should be accessible to a typical engineering graduate student with a strong background in Applied Mathematics. The main objective of these notes is to introduce a student who is familiar with concepts in linear algebra and partial differential equations to select topics in deep learning. These lecture notes exploit the strong connections between deep learning algorithms and the more conventional techniques of computational physics to achieve two goals. First, they use concepts from computational physics to develop an understanding of deep learning algorithms. Not surprisingly, many concepts in deep learning can be connected to similar concepts in computational physics, and one can utilize this connection to better understand these algorithms. Second, several novel deep learning algorithms can be used to solve challenging problems in computational physics. Thus, they offer someone who is interested in modeling a physical phenomena with a complementary set of tools.