Graph Laplacian-based Bayesian Multi-fidelity Modeling
Paper and Code
Sep 12, 2024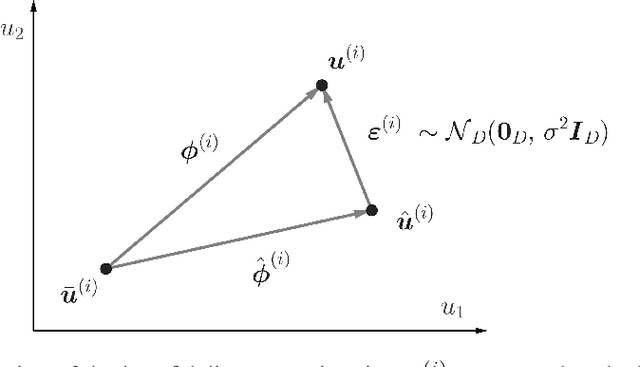


We present a novel probabilistic approach for generating multi-fidelity data while accounting for errors inherent in both low- and high-fidelity data. In this approach a graph Laplacian constructed from the low-fidelity data is used to define a multivariate Gaussian prior density for the coordinates of the true data points. In addition, few high-fidelity data points are used to construct a conjugate likelihood term. Thereafter, Bayes rule is applied to derive an explicit expression for the posterior density which is also multivariate Gaussian. The maximum \textit{a posteriori} (MAP) estimate of this density is selected to be the optimal multi-fidelity estimate. It is shown that the MAP estimate and the covariance of the posterior density can be determined through the solution of linear systems of equations. Thereafter, two methods, one based on spectral truncation and another based on a low-rank approximation, are developed to solve these equations efficiently. The multi-fidelity approach is tested on a variety of problems in solid and fluid mechanics with data that represents vectors of quantities of interest and discretized spatial fields in one and two dimensions. The results demonstrate that by utilizing a small fraction of high-fidelity data, the multi-fidelity approach can significantly improve the accuracy of a large collection of low-fidelity data points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge