A few-shot graph Laplacian-based approach for improving the accuracy of low-fidelity data
Paper and Code
Mar 29, 2023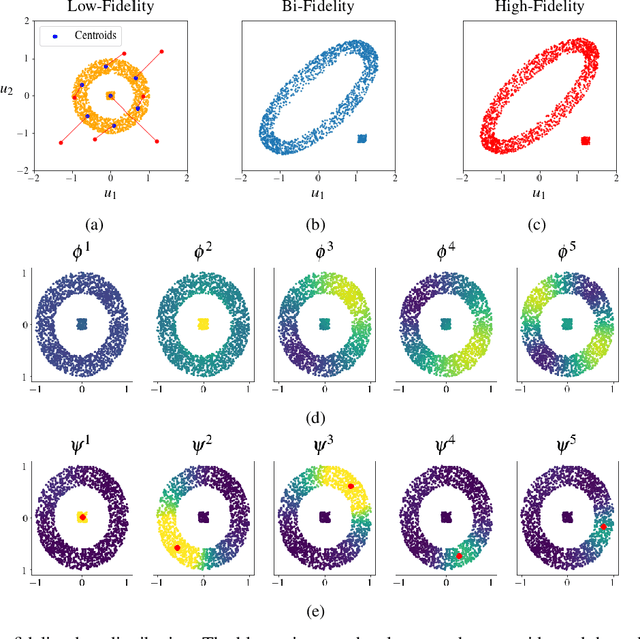

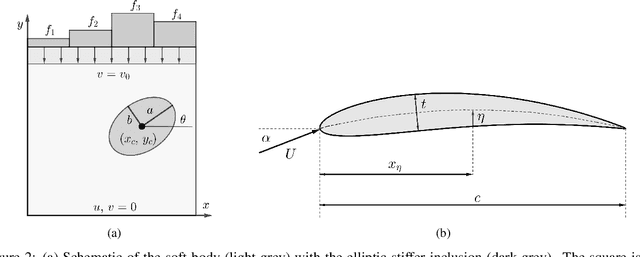

Low-fidelity data is typically inexpensive to generate but inaccurate. On the other hand, high-fidelity data is accurate but expensive to obtain. Multi-fidelity methods use a small set of high-fidelity data to enhance the accuracy of a large set of low-fidelity data. In the approach described in this paper, this is accomplished by constructing a graph Laplacian using the low-fidelity data and computing its low-lying spectrum. This spectrum is then used to cluster the data and identify points that are closest to the centroids of the clusters. High-fidelity data is then acquired for these key points. Thereafter, a transformation that maps every low-fidelity data point to its bi-fidelity counterpart is determined by minimizing the discrepancy between the bi- and high-fidelity data at the key points, and to preserve the underlying structure of the low-fidelity data distribution. The latter objective is achieved by relying, once again, on the spectral properties of the graph Laplacian. This method is applied to a problem in solid mechanics and another in aerodynamics. In both cases, this methods uses a small fraction of high-fidelity data to significantly improve the accuracy of a large set of low-fidelity data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge