Prismatic Soft Actuator Augments the Workspace of Soft Continuum Robots

Soft robots are promising for manipulation tasks thanks to their compliance, safety, and high degree of freedom. However, the commonly used bidirectional continuum segment design means soft robotic manipulators only function in a limited hemispherical workspace. This work increases a soft robotic arm's workspace by designing, fabricating, and controlling an additional soft prismatic actuator at the base of the soft arm. This actuator consists of pneumatic artificial muscles and a piston, making the actuator back-driveable. We increase the task space volume by 116\%, and we are now able to perform manipulation tasks that were previously impossible for soft robots, such as picking and placing objects at different positions on a surface and grabbing an object out of a container. By combining a soft robotic arm with a prismatic joint, we greatly increase the usability of soft robots for object manipulation. This work promotes the use of integrated and modular soft robotic systems for practical manipulation applications in human-centered environments.

Dynamic Control of Soft Manipulators to Perform Real-World Tasks

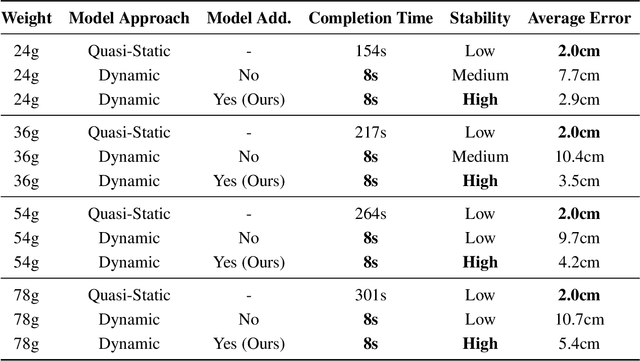
Dynamic motions are a key feature of robotic arms, enabling them to perform tasks quickly and efficiently. Soft continuum manipulators do not currently consider dynamic parameters when operating in task space. This shortcoming makes existing soft robots slow and limits their ability to deal with external forces, especially during object manipulation. We address this issue by using dynamic operational space control. Our control approach takes into account the dynamic parameters of the 3D continuum arm and introduces new models that enable multi-segment soft manipulators to operate smoothly in task space. Advanced control methods, previously afforded only to rigid robots, are now adapted to soft robots; for example, potential field avoidance was previously only shown for rigid robots and is now extended to soft robots. Using our approach, a soft manipulator can now achieve a variety of tasks that were previously not possible: we evaluate the manipulator's performance in closed-loop controlled experiments such as pick-and-place, obstacle avoidance, throwing objects using an attached soft gripper, and deliberately applying forces to a surface by drawing with a grasped piece of chalk. Besides the newly enabled skills, our approach improves tracking accuracy by 59% and increases speed by a factor of 19.3 compared to state of the art for task space control. With these newfound abilities, soft robots can start to challenge rigid robots in the field of manipulation. Our inherently safe and compliant soft robot moves the future of robotic manipulation towards a cageless setup where humans and robots work in parallel.

A Robust Adaptive Approach to Dynamic Control of Soft Continuum Manipulators

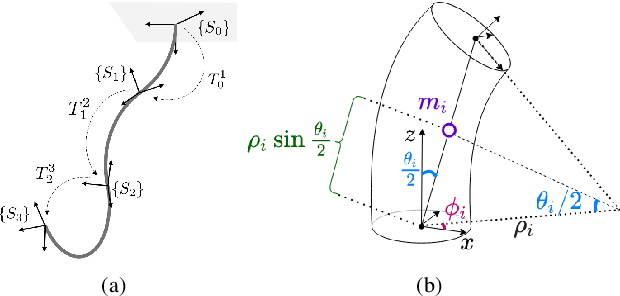
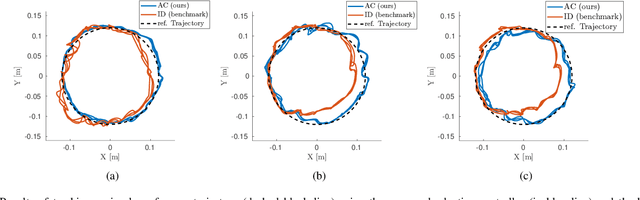
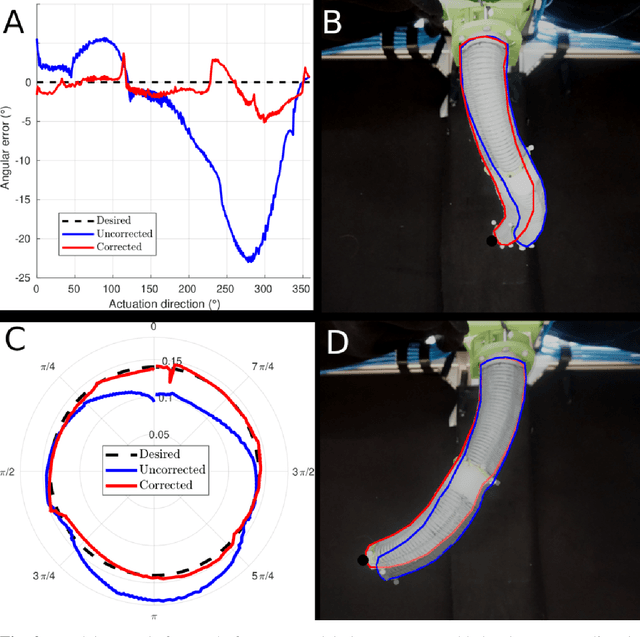
Soft robots are made of compliant and deformable materials and can perform tasks challenging for conventional rigid robots. The inherent compliance of soft robots makes them more suitable and adaptable for interactions with humans and the environment. However, this preeminence comes at a cost: their continuum nature makes it challenging to develop robust model-based control strategies. Specifically, an adaptive control approach addressing this challenge has not yet been applied to physical soft robotic arms. This work presents a reformulation of dynamics for a soft continuum manipulator using the Euler-Lagrange method. The proposed model eliminates the simplifying assumption made in previous works and provides a more accurate description of the robot's inertia. Based on our model, we introduce a task-space adaptive control scheme. This controller is robust against model parameter uncertainties and unknown input disturbances. The controller is implemented on a physical soft continuum arm. A series of experiments were carried out to validate the effectiveness of the controller in task-space trajectory tracking under different payloads. The controller outperforms the state-of-the-art method both in terms of accuracy and robustness. Moreover, the proposed model-based control design is flexible and can be generalized to any continuum robotic arm with an arbitrary number of continuum segments.