Incremental Sampling-based Motion Planners Using Policy Iteration Methods

Recent progress in randomized motion planners has led to the development of a new class of sampling-based algorithms that provide asymptotic optimality guarantees, notably the RRT* and the PRM* algorithms. Careful analysis reveals that the so-called "rewiring" step in these algorithms can be interpreted as a local policy iteration (PI) step (i.e., a local policy evaluation step followed by a local policy improvement step) so that asymptotically, as the number of samples tend to infinity, both algorithms converge to the optimal path almost surely (with probability 1). Policy iteration, along with value iteration (VI) are common methods for solving dynamic programming (DP) problems. Based on this observation, recently, the RRT$^{\#}$ algorithm has been proposed, which performs, during each iteration, Bellman updates (aka "backups") on those vertices of the graph that have the potential of being part of the optimal path (i.e., the "promising" vertices). The RRT$^{\#}$ algorithm thus utilizes dynamic programming ideas and implements them incrementally on randomly generated graphs to obtain high quality solutions. In this work, and based on this key insight, we explore a different class of dynamic programming algorithms for solving shortest-path problems on random graphs generated by iterative sampling methods. These class of algorithms utilize policy iteration instead of value iteration, and thus are better suited for massive parallelization. Contrary to the RRT* algorithm, the policy improvement during the rewiring step is not performed only locally but rather on a set of vertices that are classified as "promising" during the current iteration. This tends to speed-up the whole process. The resulting algorithm, aptly named Policy Iteration-RRT$^{\#}$ (PI-RRT$^{\#}$) is the first of a new class of DP-inspired algorithms for randomized motion planning that utilize PI methods.

Sampling-based Algorithms for Optimal Motion Planning Using Closed-loop Prediction

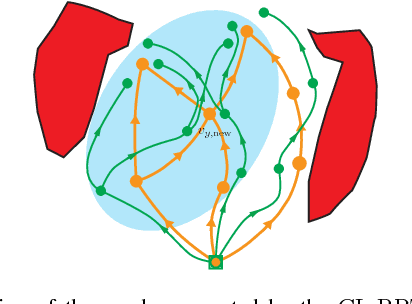
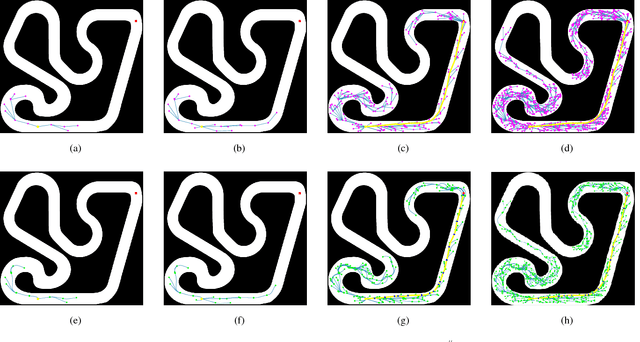
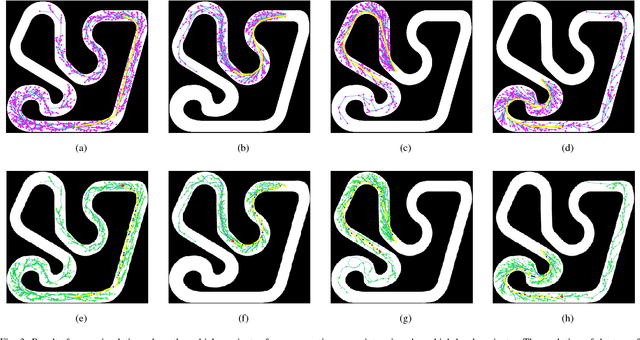
Motion planning under differential constraints, kinodynamic motion planning, is one of the canonical problems in robotics. Currently, state-of-the-art methods evolve around kinodynamic variants of popular sampling-based algorithms, such as Rapidly-exploring Random Trees (RRTs). However, there are still challenges remaining, for example, how to include complex dynamics while guaranteeing optimality. If the open-loop dynamics are unstable, exploration by random sampling in control space becomes inefficient. We describe a new sampling-based algorithm, called CL-RRT#, which leverages ideas from the RRT# algorithm and a variant of the RRT algorithm that generates trajectories using closed-loop prediction. The idea of planning with closed-loop prediction allows us to handle complex unstable dynamics and avoids the need to find computationally hard steering procedures. The search technique presented in the RRT# algorithm allows us to improve the solution quality by searching over alternative reference trajectories. Numerical simulations using a nonholonomic system demonstrate the benefits of the proposed approach.

Information-Theoretic Stochastic Optimal Control via Incremental Sampling-based Algorithms

This paper considers optimal control of dynamical systems which are represented by nonlinear stochastic differential equations. It is well-known that the optimal control policy for this problem can be obtained as a function of a value function that satisfies a nonlinear partial differential equation, namely, the Hamilton-Jacobi-Bellman equation. This nonlinear PDE must be solved backwards in time, and this computation is intractable for large scale systems. Under certain assumptions, and after applying a logarithmic transformation, an alternative characterization of the optimal policy can be given in terms of a path integral. Path Integral (PI) based control methods have recently been shown to provide elegant solutions to a broad class of stochastic optimal control problems. One of the implementation challenges with this formalism is the computation of the expectation of a cost functional over the trajectories of the unforced dynamics. Computing such expectation over trajectories that are sampled uniformly may induce numerical instabilities due to the exponentiation of the cost. Therefore, sampling of low-cost trajectories is essential for the practical implementation of PI-based methods. In this paper, we use incremental sampling-based algorithms to sample useful trajectories from the unforced system dynamics, and make a novel connection between Rapidly-exploring Random Trees (RRTs) and information-theoretic stochastic optimal control. We show the results from the numerical implementation of the proposed approach to several examples.

The Role of Vertex Consistency in Sampling-based Algorithms for Optimal Motion Planning

Motion planning problems have been studied by both the robotics and the controls research communities for a long time, and many algorithms have been developed for their solution. Among them, incremental sampling-based motion planning algorithms, such as the Rapidly-exploring Random Trees (RRTs), and the Probabilistic Road Maps (PRMs) have become very popular recently, owing to their implementation simplicity and their advantages in handling high-dimensional problems. Although these algorithms work very well in practice, the quality of the computed solution is often not good, i.e., the solution can be far from the optimal one. A recent variation of RRT, namely the RRT* algorithm, bypasses this drawback of the traditional RRT algorithm, by ensuring asymptotic optimality as the number of samples tends to infinity. Nonetheless, the convergence rate to the optimal solution may still be slow. This paper presents a new incremental sampling-based motion planning algorithm based on Rapidly-exploring Random Graphs (RRG), denoted RRT# (RRT "sharp") which also guarantees asymptotic optimality but, in addition, it also ensures that the constructed spanning tree of the geometric graph is consistent after each iteration. In consistent trees, the vertices which have the potential to be part of the optimal solution have the minimum cost-come-value. This implies that the best possible solution is readily computed if there are some vertices in the current graph that are already in the goal region. Numerical results compare with the RRT* algorithm.