GANravel: User-Driven Direction Disentanglement in Generative Adversarial Networks

Generative adversarial networks (GANs) have many application areas including image editing, domain translation, missing data imputation, and support for creative work. However, GANs are considered 'black boxes'. Specifically, the end-users have little control over how to improve editing directions through disentanglement. Prior work focused on new GAN architectures to disentangle editing directions. Alternatively, we propose GANravel a user-driven direction disentanglement tool that complements the existing GAN architectures and allows users to improve editing directions iteratively. In two user studies with 16 participants each, GANravel users were able to disentangle directions and outperformed the state-of-the-art direction discovery baselines in disentanglement performance. In the second user study, GANravel was used in a creative task of creating dog memes and was able to create high-quality edited images and GIFs.

GANzilla: User-Driven Direction Discovery in Generative Adversarial Networks

Generative Adversarial Network (GAN) is widely adopted in numerous application areas, such as data preprocessing, image editing, and creativity support. However, GAN's 'black box' nature prevents non-expert users from controlling what data a model generates, spawning a plethora of prior work that focused on algorithm-driven approaches to extract editing directions to control GAN. Complementarily, we propose a GANzilla: a user-driven tool that empowers a user with the classic scatter/gather technique to iteratively discover directions to meet their editing goals. In a study with 12 participants, GANzilla users were able to discover directions that (i) edited images to match provided examples (closed-ended tasks) and that (ii) met a high-level goal, e.g., making the face happier, while showing diversity across individuals (open-ended tasks).

An Asymptotically Optimal Algorithm for Communicating Multiplayer Multi-Armed Bandit Problems

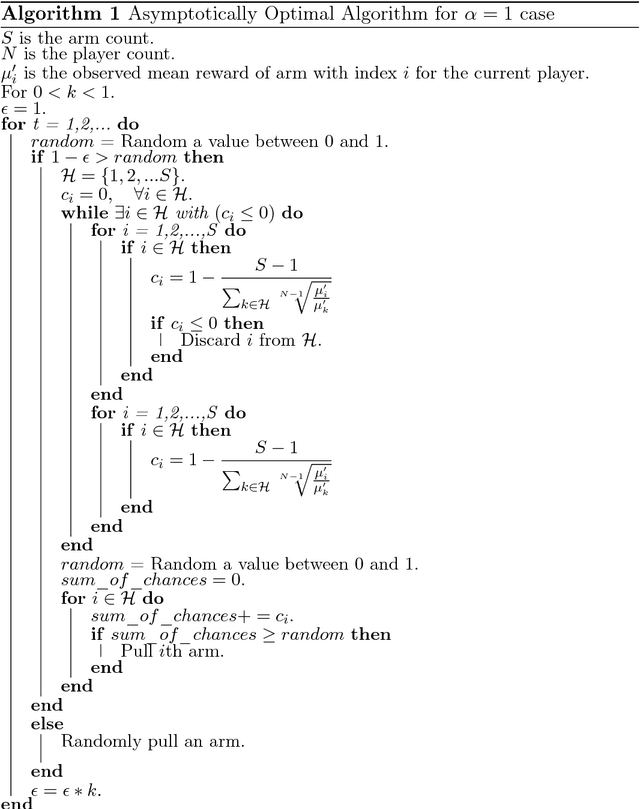
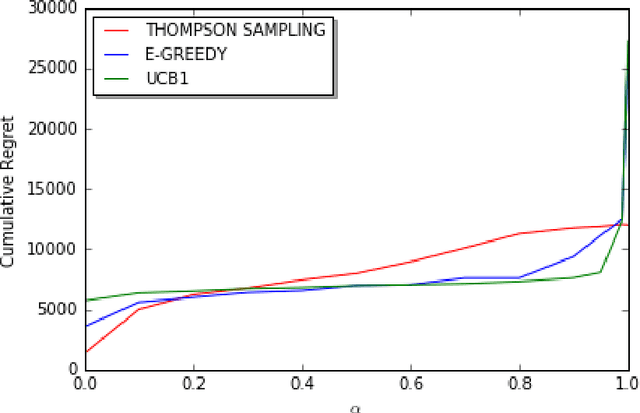
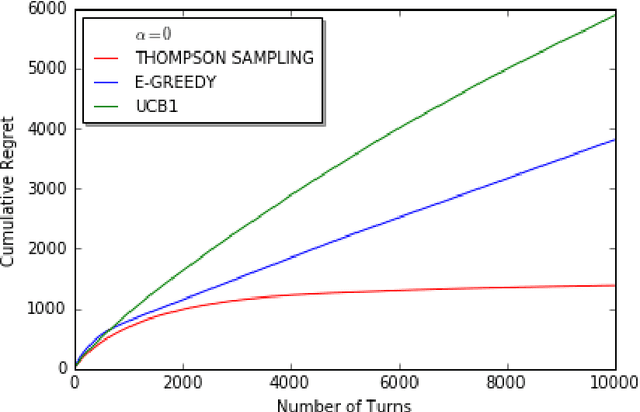
We consider a decentralized stochastic multi-armed bandit problem with multiple players. Each player aims to maximize his/her own reward by pulling an arm. The arms give rewards based on i.i.d. stochastic Bernoulli distributions. Players are not aware about the probability distributions of the arms. At the end of each turn, the players inform their neighbors about the arm he/she pulled and the reward he/she got. Neighbors of players are determined according to an Erd{\H{o}}s-R{\'e}nyi graph with connectivity $\alpha$. This graph is reproduced in the beginning of every turn with the same connectivity. When more than one player choose the same arm in a turn, we assume that only one of the players who is randomly chosen gets the reward where the others get nothing. We first start by assuming players are not aware of the collision model and offer an asymptotically optimal algorithm for $\alpha = 1$ case. Then, we extend our prior work and offer an asymptotically optimal algorithm for any connectivity but zero, assuming players aware of the collision model. We also study the effect of $\alpha$, the degree of communication between players, empirically on the cumulative regret by comparing them with traditional multi-armed bandit algorithms.

Performance Comparison of Algorithms for Movie Rating Estimation

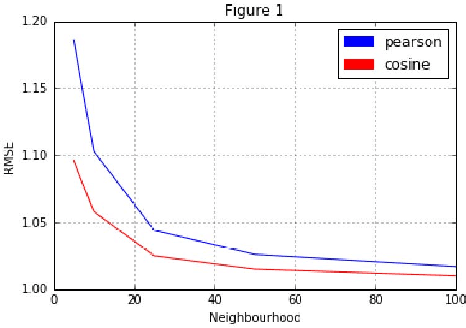
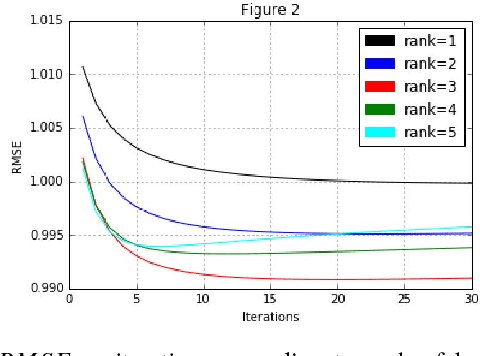
In this paper, our goal is to compare performances of three different algorithms to predict the ratings that will be given to movies by potential users where we are given a user-movie rating matrix based on the past observations. To this end, we evaluate User-Based Collaborative Filtering, Iterative Matrix Factorization and Yehuda Koren's Integrated model using neighborhood and factorization where we use root mean square error (RMSE) as the performance evaluation metric. In short, we do not observe significant differences between performances, especially when the complexity increase is considered. We can conclude that Iterative Matrix Factorization performs fairly well despite its simplicity.

The Effect of Communication on Noncooperative Multiplayer Multi-Armed Bandit Problems

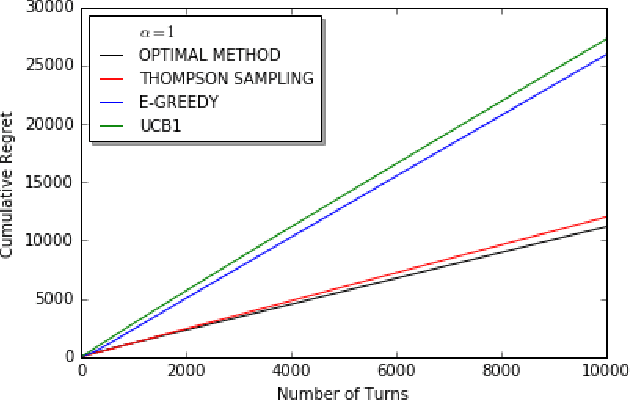
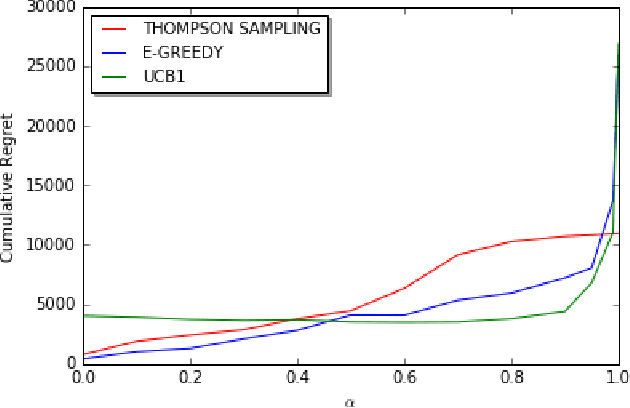
We consider decentralized stochastic multi-armed bandit problem with multiple players in the case of different communication probabilities between players. Each player makes a decision of pulling an arm without cooperation while aiming to maximize his or her reward but informs his or her neighbors in the end of every turn about the arm he or she pulled and the reward he or she got. Neighbors of players are determined according to an Erdos-Renyi graph with which is reproduced in the beginning of every turn. We consider i.i.d. rewards generated by a Bernoulli distribution and assume that players are unaware about the arms' probability distributions and their mean values. In case of a collision, we assume that only one of the players who is randomly chosen gets the reward where the others get zero reward. We study the effects of connectivity, the degree of communication between players, on the cumulative regret using well-known algorithms UCB1, epsilon-Greedy and Thompson Sampling.