An Asymptotically Optimal Algorithm for Communicating Multiplayer Multi-Armed Bandit Problems

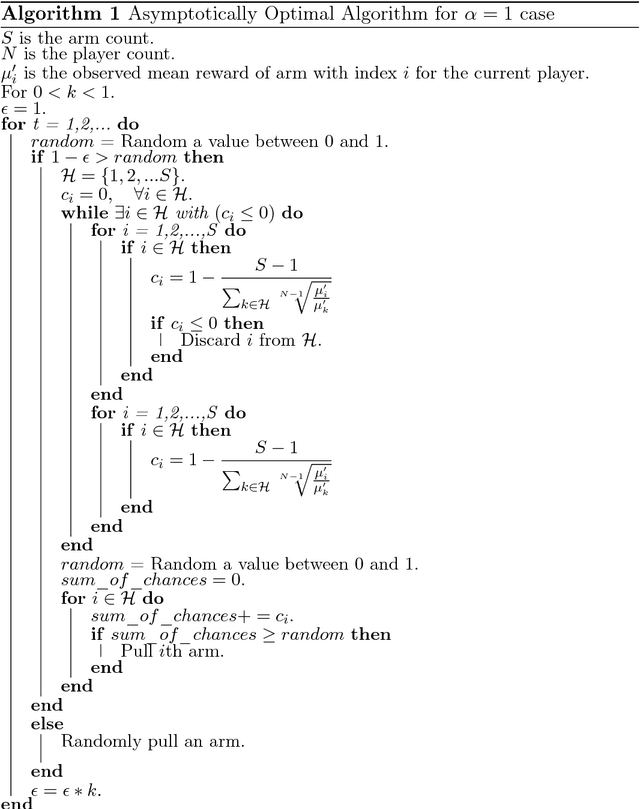
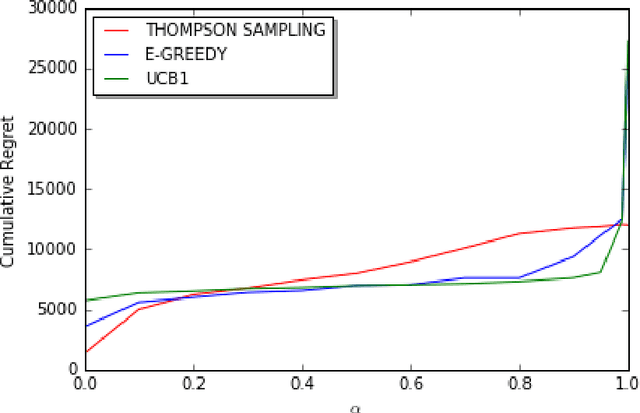
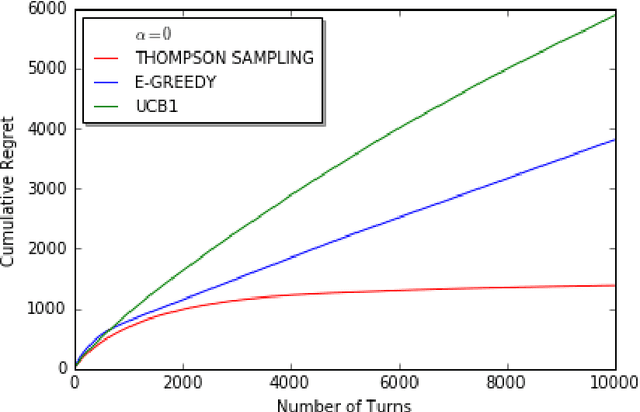
We consider a decentralized stochastic multi-armed bandit problem with multiple players. Each player aims to maximize his/her own reward by pulling an arm. The arms give rewards based on i.i.d. stochastic Bernoulli distributions. Players are not aware about the probability distributions of the arms. At the end of each turn, the players inform their neighbors about the arm he/she pulled and the reward he/she got. Neighbors of players are determined according to an Erd{\H{o}}s-R{\'e}nyi graph with connectivity $\alpha$. This graph is reproduced in the beginning of every turn with the same connectivity. When more than one player choose the same arm in a turn, we assume that only one of the players who is randomly chosen gets the reward where the others get nothing. We first start by assuming players are not aware of the collision model and offer an asymptotically optimal algorithm for $\alpha = 1$ case. Then, we extend our prior work and offer an asymptotically optimal algorithm for any connectivity but zero, assuming players aware of the collision model. We also study the effect of $\alpha$, the degree of communication between players, empirically on the cumulative regret by comparing them with traditional multi-armed bandit algorithms.