A Virtual-Force Based Swarm Algorithm for Balanced Circular Bin Packing Problems

Balanced circular bin packing problems consist in positioning a given number of weighted circles in order to minimize the radius of a circular container while satisfying equilibrium constraints. These problems are NP-hard, highly constrained and dimensional. This paper describes a swarm algorithm based on a virtual-force system in order to solve balanced circular bin packing problems. In the proposed approach, a system of forces is applied to each component allowing to take into account the constraints and minimizing the objective function using the fundamental principle of dynamics. The proposed algorithm is experimented and validated on benchmarks of various balanced circular bin packing problems with up to 300 circles. The reported results allow to assess the effectiveness of the proposed approach compared to existing results from the literature.

Hidden-Variables Genetic Algorithm for Variable-Size Design Space Optimal Layout Problems with Application to Aerospace Vehicles

The optimal layout of a complex system such as aerospace vehicles consists in placing a given number of components in a container in order to minimize one or several objectives under some geometrical or functional constraints. This paper presents an extended formulation of this problem as a variable-size design space (VSDS) problem to take into account a large number of architectural choices and components allocation during the design process. As a representative example of such systems, considering the layout of a satellite module, the VSDS aspect translates the fact that the optimizer has to choose between several subdivisions of the components. For instance, one large tank of fuel might be placed as well as two smaller tanks or three even smaller tanks for the same amount of fuel. In order to tackle this NP-hard problem, a genetic algorithm enhanced by an adapted hidden-variables mechanism is proposed. This latter is illustrated on a toy case and an aerospace application case representative to real world complexity to illustrate the performance of the proposed algorithms. The results obtained using the proposed mechanism are reported and analyzed.

Multi-fidelity modeling with different input domain definitions using Deep Gaussian Processes

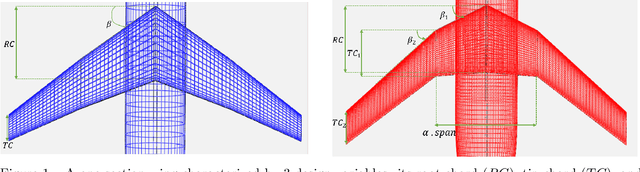
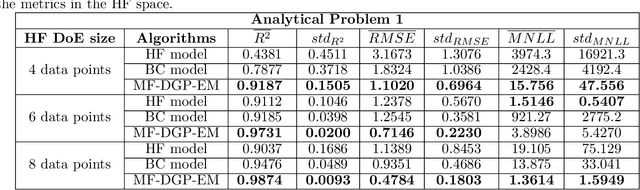
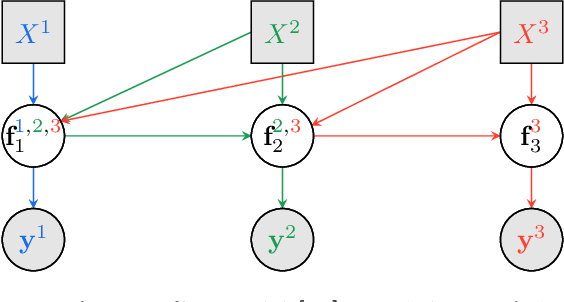
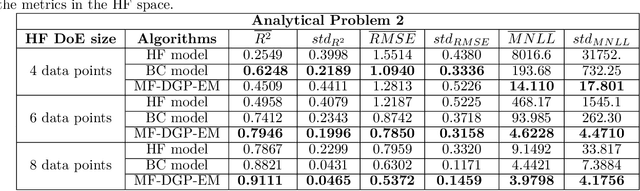
Multi-fidelity approaches combine different models built on a scarce but accurate data-set (high-fidelity data-set), and a large but approximate one (low-fidelity data-set) in order to improve the prediction accuracy. Gaussian Processes (GPs) are one of the popular approaches to exhibit the correlations between these different fidelity levels. Deep Gaussian Processes (DGPs) that are functional compositions of GPs have also been adapted to multi-fidelity using the Multi-Fidelity Deep Gaussian process model (MF-DGP). This model increases the expressive power compared to GPs by considering non-linear correlations between fidelities within a Bayesian framework. However, these multi-fidelity methods consider only the case where the inputs of the different fidelity models are defined over the same domain of definition (e.g., same variables, same dimensions). However, due to simplification in the modeling of the low-fidelity, some variables may be omitted or a different parametrization may be used compared to the high-fidelity model. In this paper, Deep Gaussian Processes for multi-fidelity (MF-DGP) are extended to the case where a different parametrization is used for each fidelity. The performance of the proposed multifidelity modeling technique is assessed on analytical test cases and on structural and aerodynamic real physical problems.

Bayesian Optimization using Deep Gaussian Processes

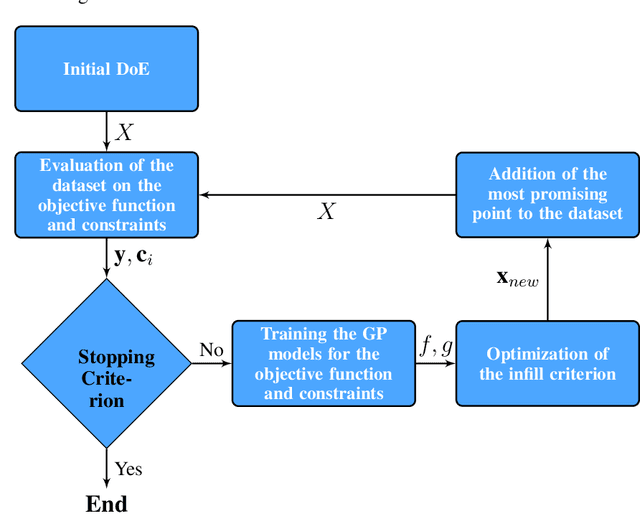
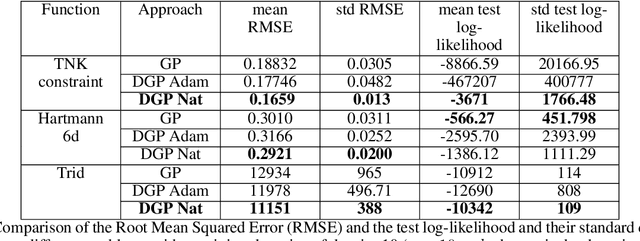
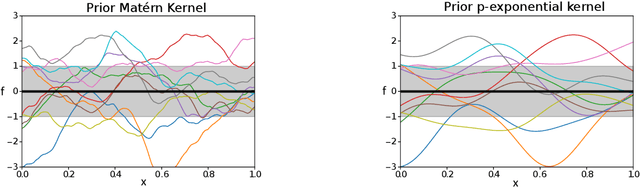
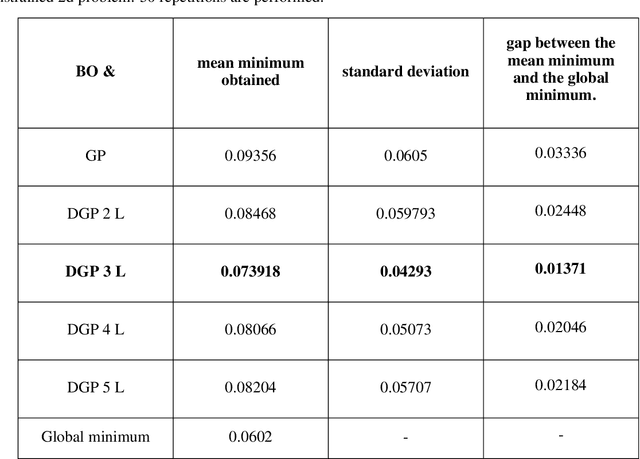
Bayesian Optimization using Gaussian Processes is a popular approach to deal with the optimization of expensive black-box functions. However, because of the a priori on the stationarity of the covariance matrix of classic Gaussian Processes, this method may not be adapted for non-stationary functions involved in the optimization problem. To overcome this issue, a new Bayesian Optimization approach is proposed. It is based on Deep Gaussian Processes as surrogate models instead of classic Gaussian Processes. This modeling technique increases the power of representation to capture the non-stationarity by simply considering a functional composition of stationary Gaussian Processes, providing a multiple layer structure. This paper proposes a new algorithm for Global Optimization by coupling Deep Gaussian Processes and Bayesian Optimization. The specificities of this optimization method are discussed and highlighted with academic test cases. The performance of the proposed algorithm is assessed on analytical test cases and an aerospace design optimization problem and compared to the state-of-the-art stationary and non-stationary Bayesian Optimization approaches.

Efficient Global Optimization using Deep Gaussian Processes

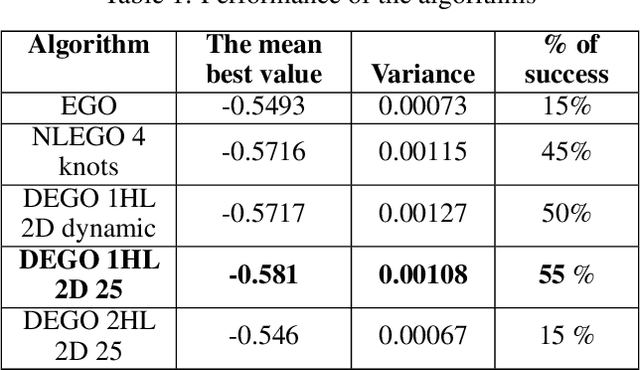
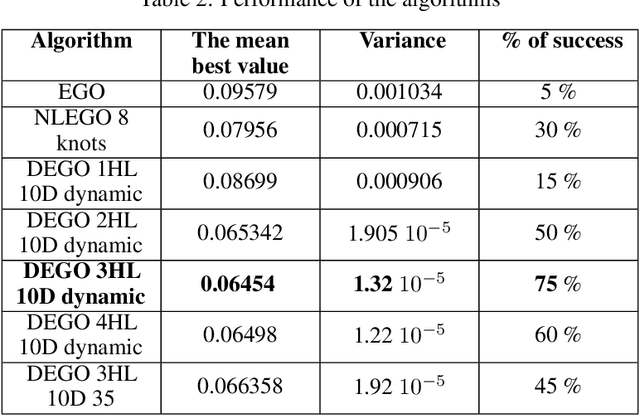
Efficient Global Optimization (EGO) is widely used for the optimization of computationally expensive black-box functions. It uses a surrogate modeling technique based on Gaussian Processes (Kriging). However, due to the use of a stationary covariance, Kriging is not well suited for approximating non stationary functions. This paper explores the integration of Deep Gaussian processes (DGP) in EGO framework to deal with the non-stationary issues and investigates the induced challenges and opportunities. Numerical experimentations are performed on analytical problems to highlight the different aspects of DGP and EGO.

An Adaptative Multi-GPU based Branch-and-Bound. A Case Study: the Flow-Shop Scheduling Problem

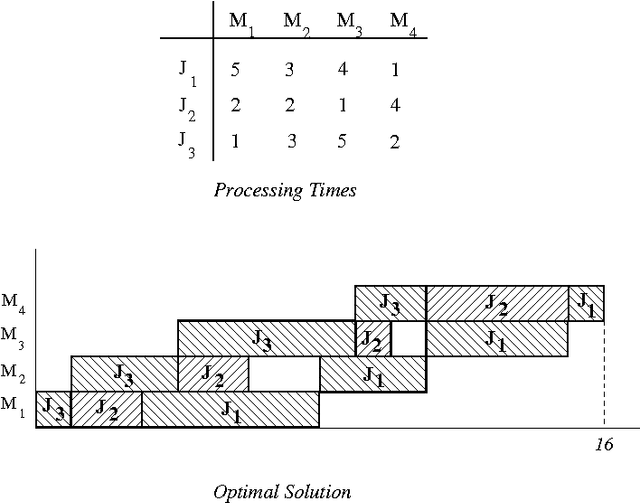
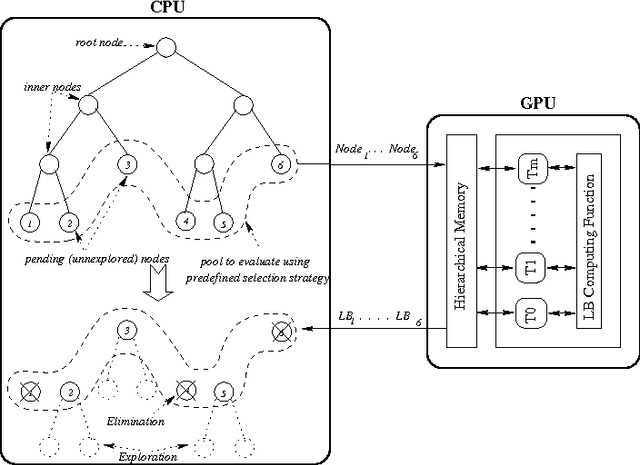
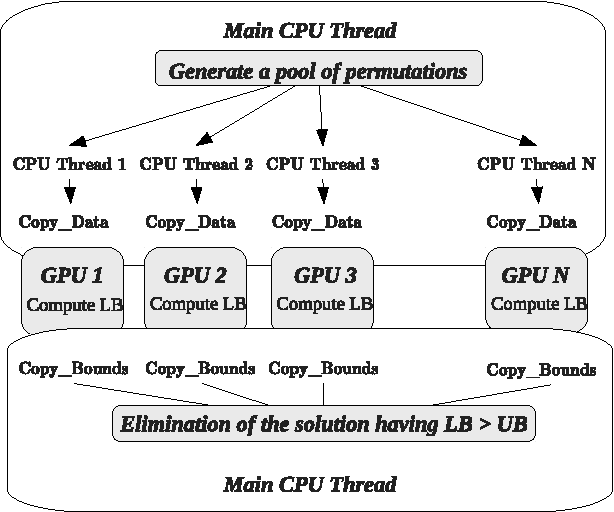
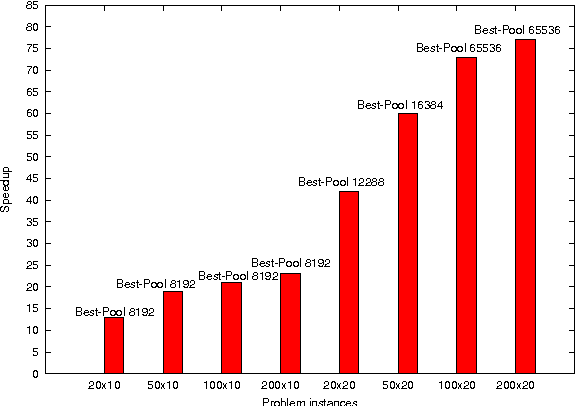
Solving exactly Combinatorial Optimization Problems (COPs) using a Branch-and-Bound (B&B) algorithm requires a huge amount of computational resources. Therefore, we recently investigated designing B&B algorithms on top of graphics processing units (GPUs) using a parallel bounding model. The proposed model assumes parallelizing the evaluation of the lower bounds on pools of sub-problems. The results demonstrated that the size of the evaluated pool has a significant impact on the performance of B&B and that it depends strongly on the problem instance being solved. In this paper, we design an adaptative parallel B&B algorithm for solving permutation-based combinatorial optimization problems such as FSP (Flow-shop Scheduling Problem) on GPU accelerators. To do so, we propose a dynamic heuristic for parameter auto-tuning at runtime. Another challenge of this work is to exploit larger degrees of parallelism by using the combined computational power of multiple GPU devices. The approach has been applied to the permutation flow-shop problem. Extensive experiments have been carried out on well-known FSP benchmarks using an Nvidia Tesla S1070 Computing System equipped with two Tesla T10 GPUs. Compared to a CPU-based execution, accelerations up to 105 are achieved for large problem instances.