Multi-fidelity modeling with different input domain definitions using Deep Gaussian Processes

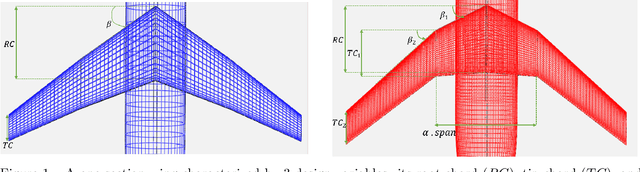
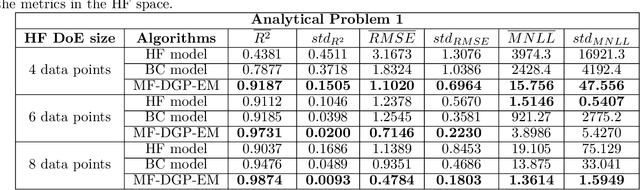
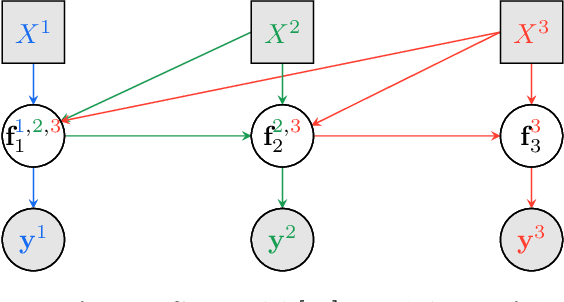
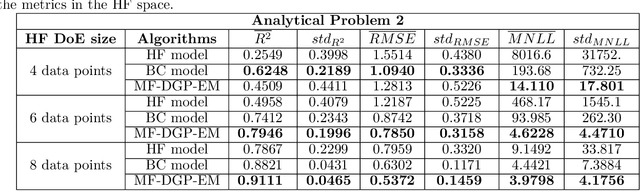
Multi-fidelity approaches combine different models built on a scarce but accurate data-set (high-fidelity data-set), and a large but approximate one (low-fidelity data-set) in order to improve the prediction accuracy. Gaussian Processes (GPs) are one of the popular approaches to exhibit the correlations between these different fidelity levels. Deep Gaussian Processes (DGPs) that are functional compositions of GPs have also been adapted to multi-fidelity using the Multi-Fidelity Deep Gaussian process model (MF-DGP). This model increases the expressive power compared to GPs by considering non-linear correlations between fidelities within a Bayesian framework. However, these multi-fidelity methods consider only the case where the inputs of the different fidelity models are defined over the same domain of definition (e.g., same variables, same dimensions). However, due to simplification in the modeling of the low-fidelity, some variables may be omitted or a different parametrization may be used compared to the high-fidelity model. In this paper, Deep Gaussian Processes for multi-fidelity (MF-DGP) are extended to the case where a different parametrization is used for each fidelity. The performance of the proposed multifidelity modeling technique is assessed on analytical test cases and on structural and aerodynamic real physical problems.

Bayesian optimization of variable-size design space problems

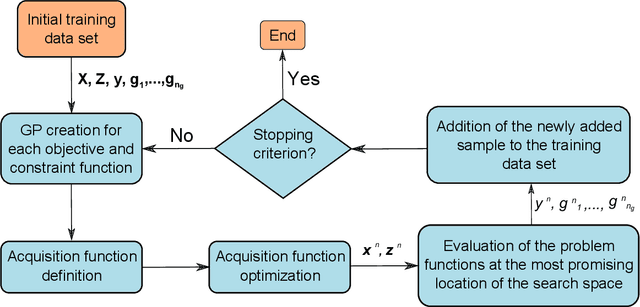
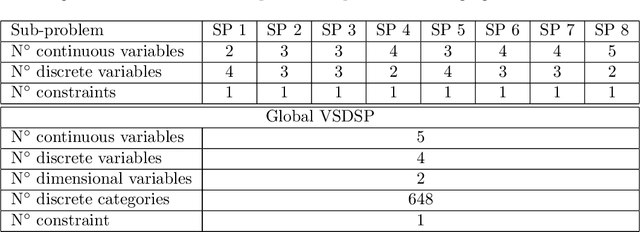
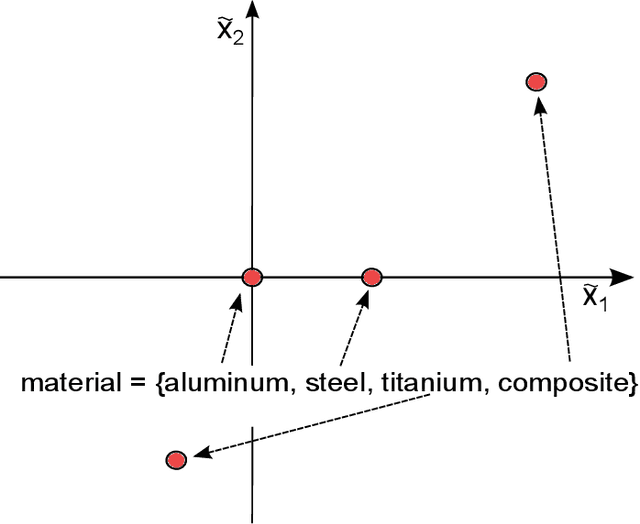
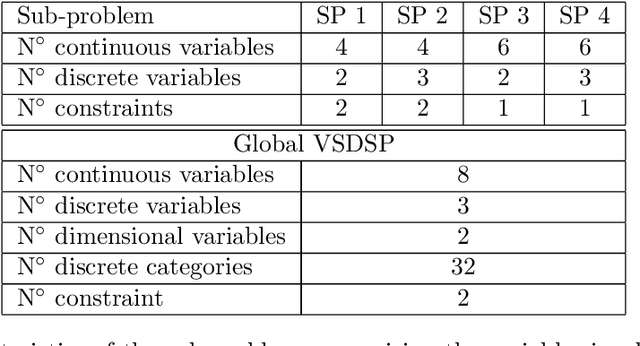
Within the framework of complex system design, it is often necessary to solve mixed variable optimization problems, in which the objective and constraint functions can depend simultaneously on continuous and discrete variables. Additionally, complex system design problems occasionally present a variable-size design space. This results in an optimization problem for which the search space varies dynamically (with respect to both number and type of variables) along the optimization process as a function of the values of specific discrete decision variables. Similarly, the number and type of constraints can vary as well. In this paper, two alternative Bayesian Optimization-based approaches are proposed in order to solve this type of optimization problems. The first one consists in a budget allocation strategy allowing to focus the computational budget on the most promising design sub-spaces. The second approach, instead, is based on the definition of a kernel function allowing to compute the covariance between samples characterized by partially different sets of variables. The results obtained on analytical and engineering related test-cases show a faster and more consistent convergence of both proposed methods with respect to the standard approaches.

Bayesian Optimization using Deep Gaussian Processes

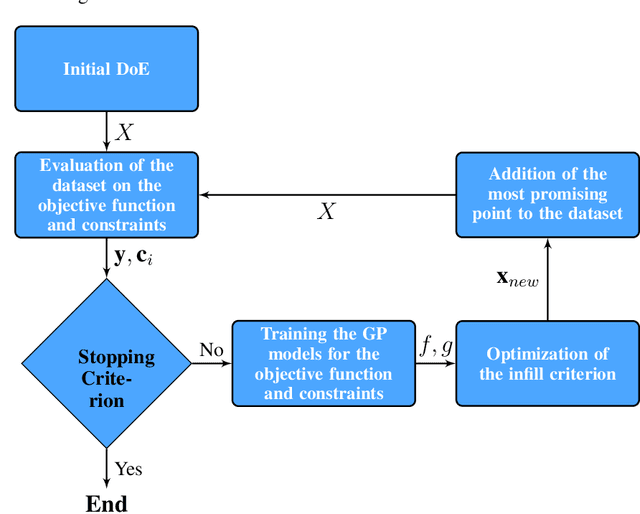
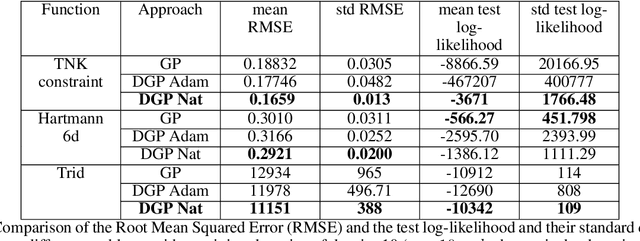
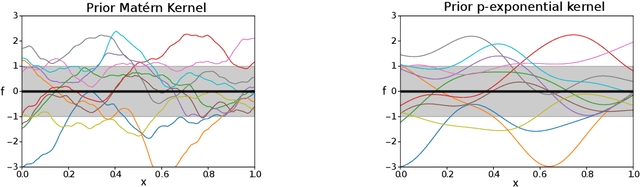
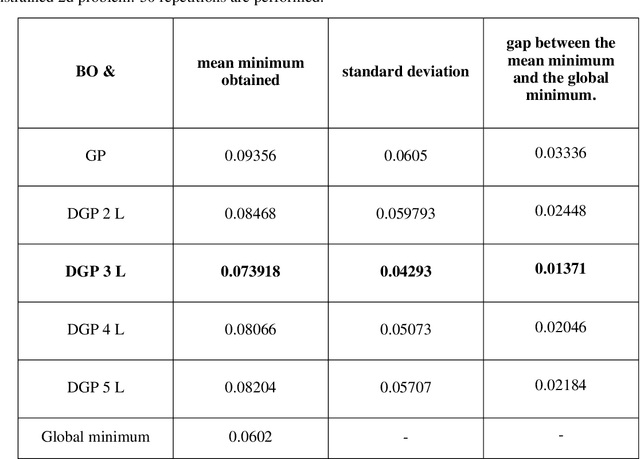
Bayesian Optimization using Gaussian Processes is a popular approach to deal with the optimization of expensive black-box functions. However, because of the a priori on the stationarity of the covariance matrix of classic Gaussian Processes, this method may not be adapted for non-stationary functions involved in the optimization problem. To overcome this issue, a new Bayesian Optimization approach is proposed. It is based on Deep Gaussian Processes as surrogate models instead of classic Gaussian Processes. This modeling technique increases the power of representation to capture the non-stationarity by simply considering a functional composition of stationary Gaussian Processes, providing a multiple layer structure. This paper proposes a new algorithm for Global Optimization by coupling Deep Gaussian Processes and Bayesian Optimization. The specificities of this optimization method are discussed and highlighted with academic test cases. The performance of the proposed algorithm is assessed on analytical test cases and an aerospace design optimization problem and compared to the state-of-the-art stationary and non-stationary Bayesian Optimization approaches.

Efficient Global Optimization using Deep Gaussian Processes

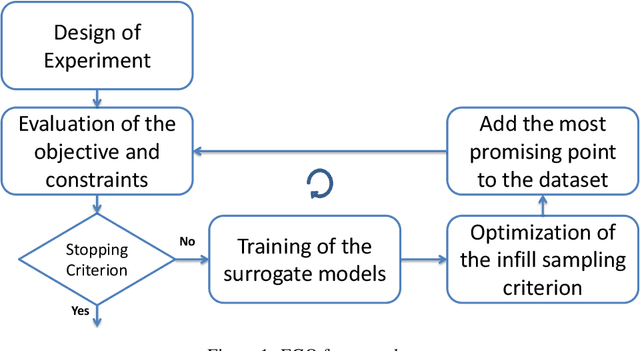
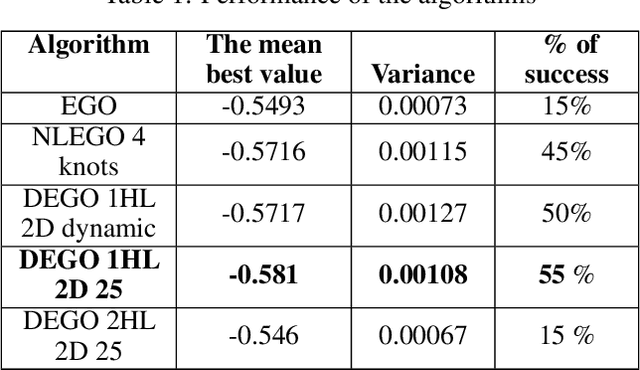
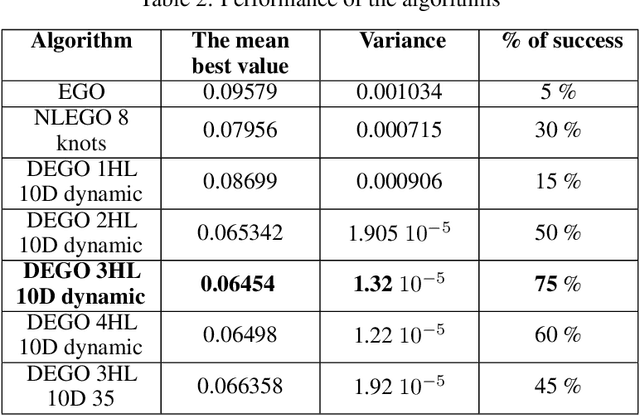
Efficient Global Optimization (EGO) is widely used for the optimization of computationally expensive black-box functions. It uses a surrogate modeling technique based on Gaussian Processes (Kriging). However, due to the use of a stationary covariance, Kriging is not well suited for approximating non stationary functions. This paper explores the integration of Deep Gaussian processes (DGP) in EGO framework to deal with the non-stationary issues and investigates the induced challenges and opportunities. Numerical experimentations are performed on analytical problems to highlight the different aspects of DGP and EGO.