Connected and Automated Vehicles in Mixed-Traffic: Learning Human Driver Behavior for Effective On-Ramp Merging

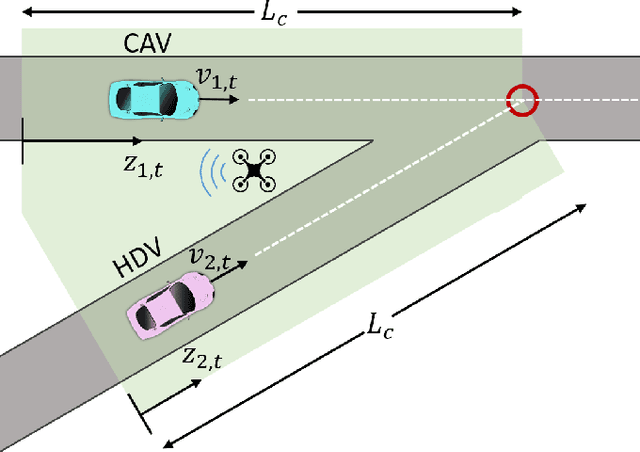
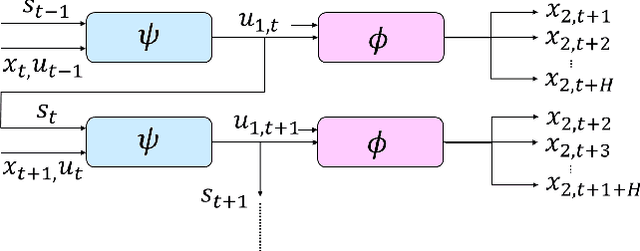
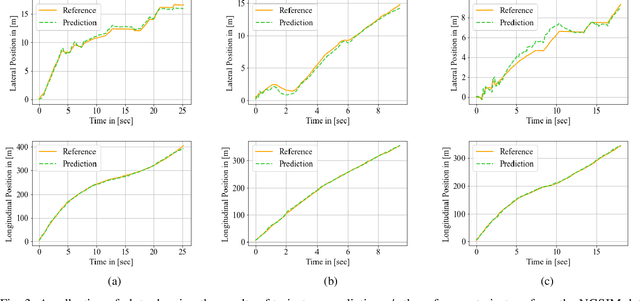
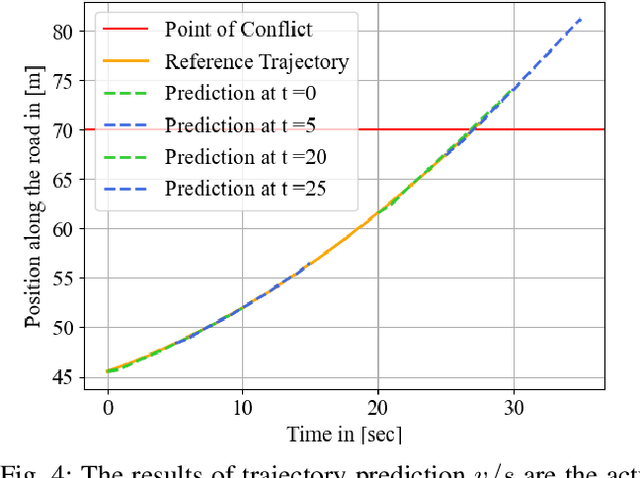
Highway merging scenarios featuring mixed traffic conditions pose significant modeling and control challenges for connected and automated vehicles (CAVs) interacting with incoming on-ramp human-driven vehicles (HDVs). In this paper, we present an approach to learn an approximate information state model of CAV-HDV interactions for a CAV to maneuver safely during highway merging. In our approach, the CAV learns the behavior of an incoming HDV using approximate information states before generating a control strategy to facilitate merging. First, we validate the efficacy of this framework on real-world data by using it to predict the behavior of an HDV in mixed traffic situations extracted from the Next-Generation Simulation repository. Then, we generate simulation data for HDV-CAV interactions in a highway merging scenario using a standard inverse reinforcement learning approach. Without assuming a prior knowledge of the generating model, we show that our approximate information state model learns to predict the future trajectory of the HDV using only observations. Subsequently, we generate safe control policies for a CAV while merging with HDVs, demonstrating a spectrum of driving behaviors, from aggressive to conservative. We demonstrate the effectiveness of the proposed approach by performing numerical simulations.

Worst-Case Control and Learning Using Partial Observations Over an Infinite Time-Horizon

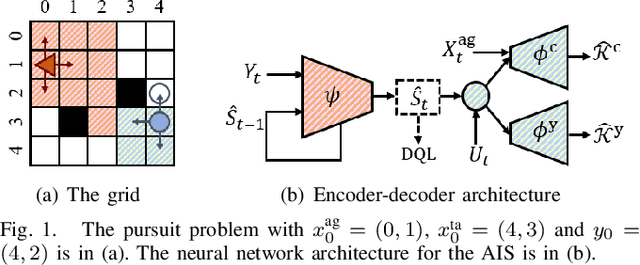
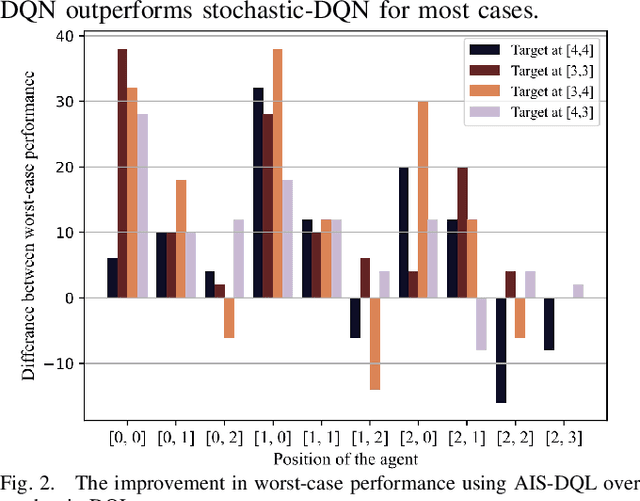
Safety-critical cyber-physical systems require control strategies whose worst-case performance is robust against adversarial disturbances and modeling uncertainties. In this paper, we present a framework for approximate control and learning in partially observed systems to minimize the worst-case discounted cost over an infinite time horizon. We model disturbances to the system as finite-valued uncertain variables with unknown probability distributions. For problems with known system dynamics, we construct a dynamic programming (DP) decomposition to compute the optimal control strategy. Our first contribution is to define information states that improve the computational tractability of this DP without loss of optimality. Then, we describe a simplification for a class of problems where the incurred cost is observable at each time instance. Our second contribution is defining an approximate information state that can be constructed or learned directly from observed data for problems with observable costs. We derive bounds on the performance loss of the resulting approximate control strategy and illustrate the effectiveness of our approach in partially observed decision-making problems with a numerical example.

Approximate Information States for Worst-Case Control and Learning in Uncertain Systems

In this paper, we investigate discrete-time decision-making problems in uncertain systems with partially observed states. We consider a non-stochastic model, where uncontrolled disturbances acting on the system take values in bounded sets with unknown distributions. We present a general framework for decision-making in such problems by developing the notions of information states and approximate information states. In our definition of an information state, we introduce conditions to identify for an uncertain variable sufficient to construct a dynamic program (DP) that computes an optimal strategy. We show that many information states from the literature on worst-case control actions, e.g., the conditional range, are examples of our more general definition. Next, we relax these conditions to define approximate information states using only output variables, which can be learned from output data without knowledge of system dynamics. We use this notion to formulate an approximate DP that yields a strategy with a bounded performance loss. Finally, we illustrate the application of our results in control and reinforcement learning using numerical examples.