Mitigating Position-Shift Failures in Text-Based Modular Arithmetic via Position Curriculum and Template Diversity

Building on insights from the grokking literature, we study character-level Transformers trained to compute modular addition from text, and focus on robustness under input-format variation rather than only in-distribution accuracy. We identify a previously under-emphasized failure mode: models that achieve high in-distribution accuracy can fail catastrophically when the same expression is shifted to different absolute character positions ("position shift") or presented under out-of-distribution natural-language templates. Using a disjoint-pair split over all ordered pairs for p=97, we show that a baseline model reaches strong in-distribution performance yet collapses under position shift and template OOD. We then introduce a simple training recipe that combines (i) explicit expression boundary markers, (ii) position curriculum that broadens the range of absolute positions seen during training, (iii) diverse template mixtures, and (iv) consistency training across multiple variants per example. Across three seeds, this intervention substantially improves robustness to position shift and template OOD while maintaining high in-distribution accuracy, whereas an ALiBi-style ablation fails to learn the task under our setup. Our results suggest that steering procedural generalization under noisy supervision benefits from explicitly training invariances that are otherwise absent from the data distribution, and we provide a reproducible evaluation protocol and artifacts.

DyKAF: Dynamical Kronecker Approximation of the Fisher Information Matrix for Gradient Preconditioning

Recently, optimizers that explicitly treat weights as matrices, rather than flattened vectors, have demonstrated their effectiveness. This perspective naturally leads to structured approximations of the Fisher matrix as preconditioners, where the matrix view induces a Kronecker-factorized form that enables memory-efficient representation. However, constructing such approximations both efficiently and accurately remains an open challenge, since obtaining the optimal factorization is resource-intensive and practical methods therefore rely on heuristic design choices. In this work, we introduce a novel approach that leverages projector-splitting integrators to construct effective preconditioners. Our optimizer, DyKAF (Dynamical Kronecker Approximation of the Fisher Matrix), consistently improves the Fisher matrix approximation quality. Experiments on large language model pre-training and fine-tuning demonstrate that DyKAF outperforms existing optimizers across a range of evaluation metrics.

Pay Attention to Attention Distribution: A New Local Lipschitz Bound for Transformers

We present a novel local Lipschitz bound for self-attention blocks of transformers. This bound is based on a refined closed-form expression for the spectral norm of the softmax function. The resulting bound is not only more accurate than in the prior art, but also unveils the dependence of the Lipschitz constant on attention score maps. Based on the new findings, we suggest an explanation of the way distributions inside the attention map affect the robustness from the Lipschitz constant perspective. We also introduce a new lightweight regularization term called JaSMin (Jacobian Softmax norm Minimization), which boosts the transformer's robustness and decreases local Lipschitz constants of the whole network.

Group and Shuffle: Efficient Structured Orthogonal Parametrization

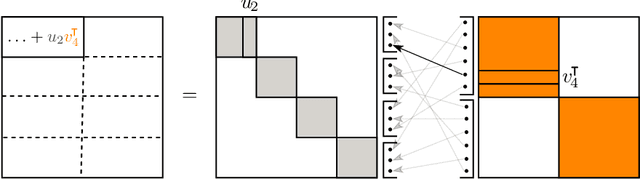
The increasing size of neural networks has led to a growing demand for methods of efficient fine-tuning. Recently, an orthogonal fine-tuning paradigm was introduced that uses orthogonal matrices for adapting the weights of a pretrained model. In this paper, we introduce a new class of structured matrices, which unifies and generalizes structured classes from previous works. We examine properties of this class and build a structured orthogonal parametrization upon it. We then use this parametrization to modify the orthogonal fine-tuning framework, improving parameter and computational efficiency. We empirically validate our method on different domains, including adapting of text-to-image diffusion models and downstream task fine-tuning in language modeling. Additionally, we adapt our construction for orthogonal convolutions and conduct experiments with 1-Lipschitz neural networks.