A Theory of I/O-Efficient Sparse Neural Network Inference

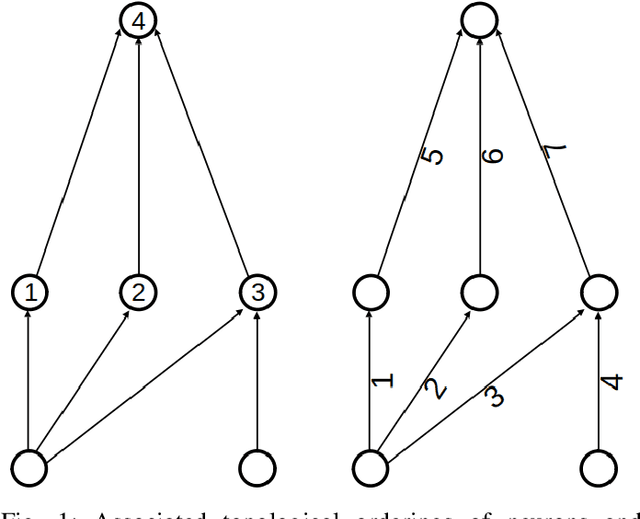
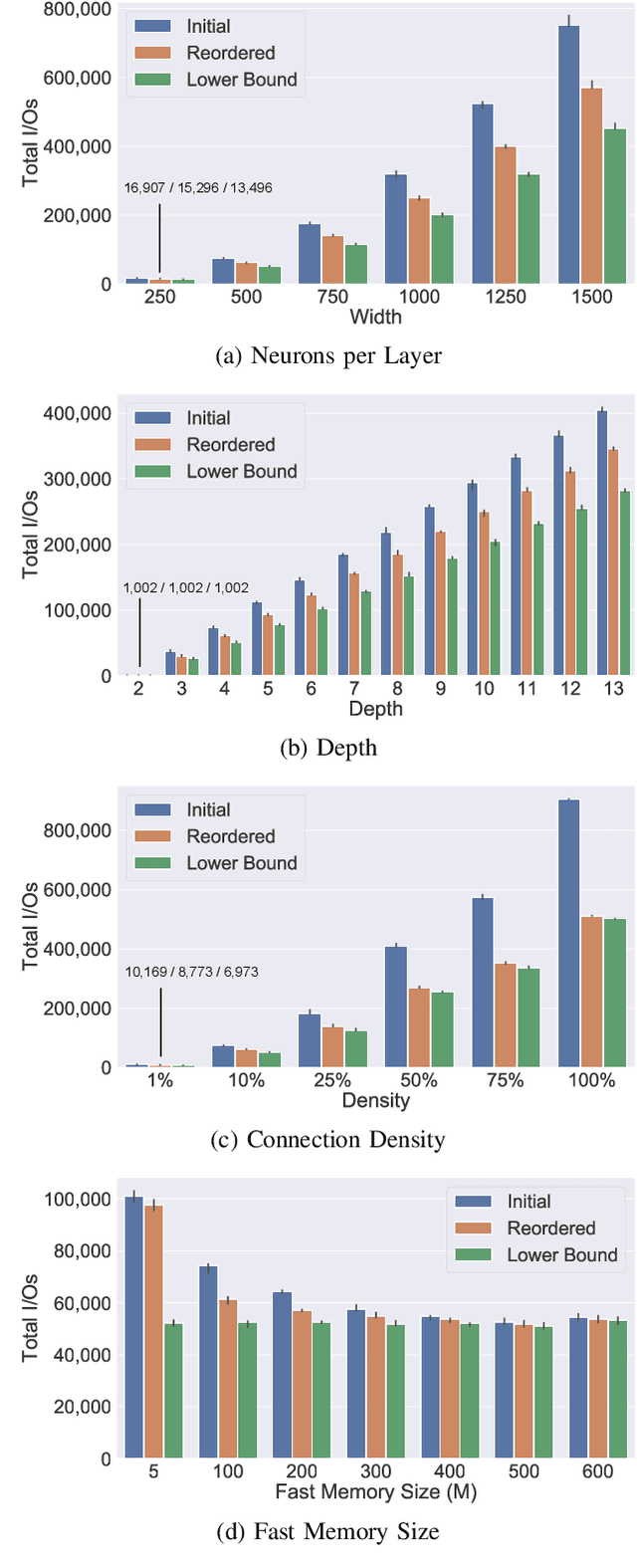
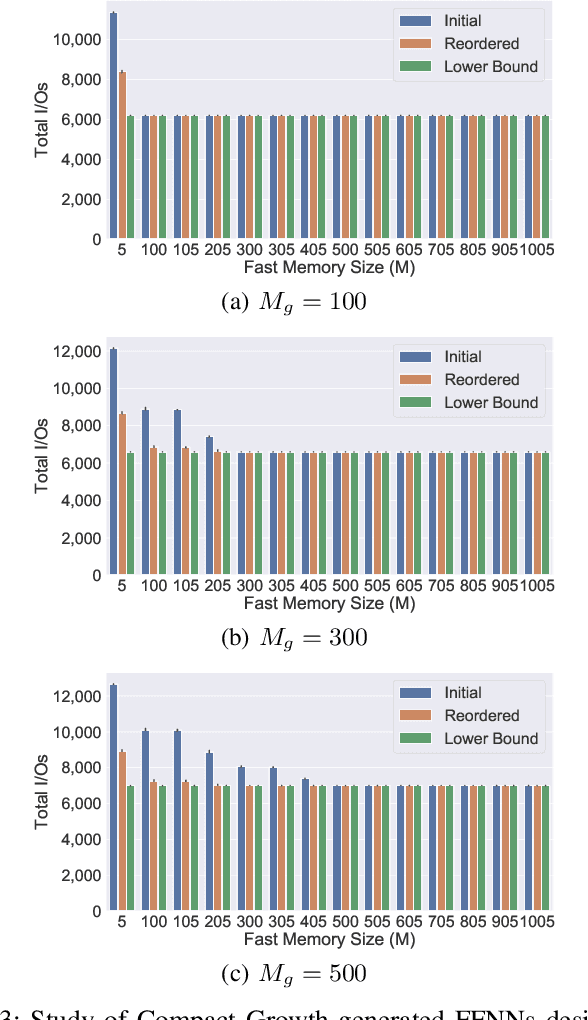
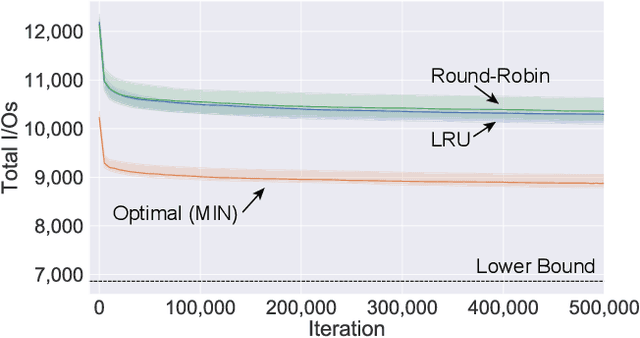
As the accuracy of machine learning models increases at a fast rate, so does their demand for energy and compute resources. On a low level, the major part of these resources is consumed by data movement between different memory units. Modern hardware architectures contain a form of fast memory (e.g., cache, registers), which is small, and a slow memory (e.g., DRAM), which is larger but expensive to access. We can only process data that is stored in fast memory, which incurs data movement (input/output-operations, or I/Os) between the two units. In this paper, we provide a rigorous theoretical analysis of the I/Os needed in sparse feedforward neural network (FFNN) inference. We establish bounds that determine the optimal number of I/Os up to a factor of 2 and present a method that uses a number of I/Os within that range. Much of the I/O-complexity is determined by a few high-level properties of the FFNN (number of inputs, outputs, neurons, and connections), but if we want to get closer to the exact lower bound, the instance-specific sparsity patterns need to be considered. Departing from the 2-optimal computation strategy, we show how to reduce the number of I/Os further with simulated annealing. Complementing this result, we provide an algorithm that constructively generates networks with maximum I/O-efficiency for inference. We test the algorithms and empirically verify our theoretical and algorithmic contributions. In our experiments on real hardware we observe speedups of up to 45$\times$ relative to the standard way of performing inference.

Underestimated cost of targeted attacks on complex networks

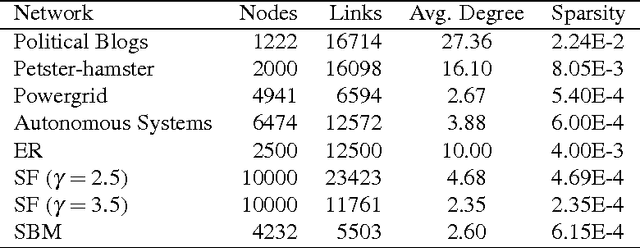
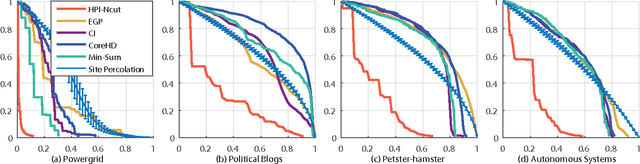
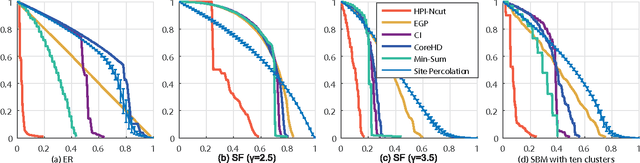
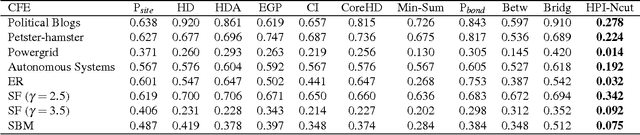
The robustness of complex networks under targeted attacks is deeply connected to the resilience of complex systems, i.e., the ability to make appropriate responses to the attacks. In this article, we investigated the state-of-the-art targeted node attack algorithms and demonstrate that they become very inefficient when the cost of the attack is taken into consideration. In this paper, we made explicit assumption that the cost of removing a node is proportional to the number of adjacent links that are removed, i.e., higher degree nodes have higher cost. Finally, for the case when it is possible to attack links, we propose a simple and efficient edge removal strategy named Hierarchical Power Iterative Normalized cut (HPI-Ncut).The results on real and artificial networks show that the HPI-Ncut algorithm outperforms all the node removal and link removal attack algorithms when the cost of the attack is taken into consideration. In addition, we show that on sparse networks, the complexity of this hierarchical power iteration edge removal algorithm is only $O(n\log^{2+\epsilon}(n))$.