Inferring short-term volatility indicators from Bitcoin blockchain

In this paper, we study the possibility of inferring early warning indicators (EWIs) for periods of extreme bitcoin price volatility using features obtained from Bitcoin daily transaction graphs. We infer the low-dimensional representations of transaction graphs in the time period from 2012 to 2017 using Bitcoin blockchain, and demonstrate how these representations can be used to predict extreme price volatility events. Our EWI, which is obtained with a non-negative decomposition, contains more predictive information than those obtained with singular value decomposition or scalar value of the total Bitcoin transaction volume.

Underestimated cost of targeted attacks on complex networks

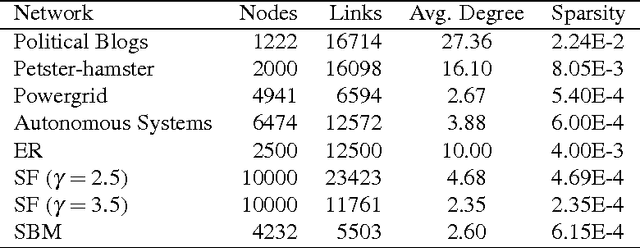
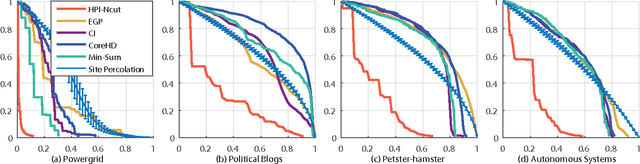
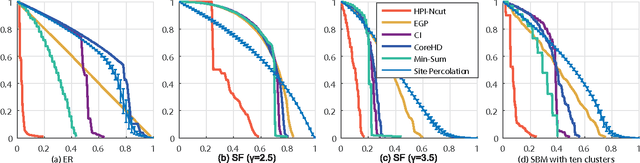
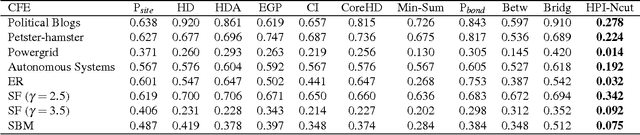
The robustness of complex networks under targeted attacks is deeply connected to the resilience of complex systems, i.e., the ability to make appropriate responses to the attacks. In this article, we investigated the state-of-the-art targeted node attack algorithms and demonstrate that they become very inefficient when the cost of the attack is taken into consideration. In this paper, we made explicit assumption that the cost of removing a node is proportional to the number of adjacent links that are removed, i.e., higher degree nodes have higher cost. Finally, for the case when it is possible to attack links, we propose a simple and efficient edge removal strategy named Hierarchical Power Iterative Normalized cut (HPI-Ncut).The results on real and artificial networks show that the HPI-Ncut algorithm outperforms all the node removal and link removal attack algorithms when the cost of the attack is taken into consideration. In addition, we show that on sparse networks, the complexity of this hierarchical power iteration edge removal algorithm is only $O(n\log^{2+\epsilon}(n))$.

A Nonlinear Orthogonal Non-Negative Matrix Factorization Approach to Subspace Clustering

A recent theoretical analysis shows the equivalence between non-negative matrix factorization (NMF) and spectral clustering based approach to subspace clustering. As NMF and many of its variants are essentially linear, we introduce a nonlinear NMF with explicit orthogonality and derive general kernel-based orthogonal multiplicative update rules to solve the subspace clustering problem. In nonlinear orthogonal NMF framework, we propose two subspace clustering algorithms, named kernel-based non-negative subspace clustering KNSC-Ncut and KNSC-Rcut and establish their connection with spectral normalized cut and ratio cut clustering. We further extend the nonlinear orthogonal NMF framework and introduce a graph regularization to obtain a factorization that respects a local geometric structure of the data after the nonlinear mapping. The proposed NMF-based approach to subspace clustering takes into account the nonlinear nature of the manifold, as well as its intrinsic local geometry, which considerably improves the clustering performance when compared to the several recently proposed state-of-the-art methods.