Underestimated cost of targeted attacks on complex networks
Paper and Code
Oct 10, 2017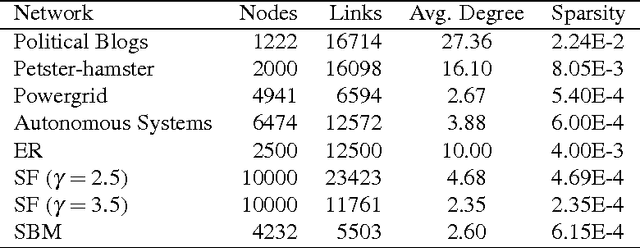
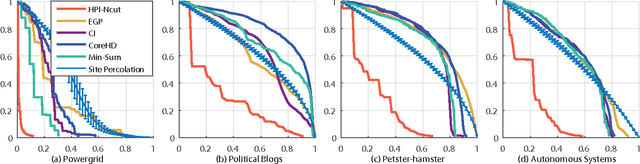
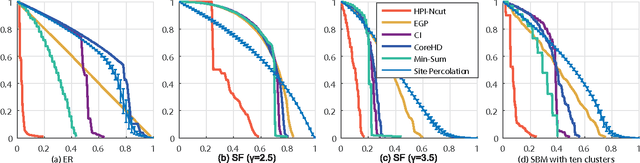
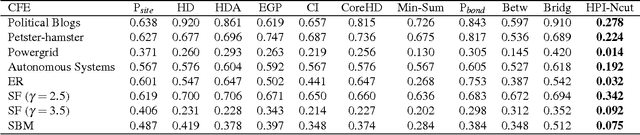
The robustness of complex networks under targeted attacks is deeply connected to the resilience of complex systems, i.e., the ability to make appropriate responses to the attacks. In this article, we investigated the state-of-the-art targeted node attack algorithms and demonstrate that they become very inefficient when the cost of the attack is taken into consideration. In this paper, we made explicit assumption that the cost of removing a node is proportional to the number of adjacent links that are removed, i.e., higher degree nodes have higher cost. Finally, for the case when it is possible to attack links, we propose a simple and efficient edge removal strategy named Hierarchical Power Iterative Normalized cut (HPI-Ncut).The results on real and artificial networks show that the HPI-Ncut algorithm outperforms all the node removal and link removal attack algorithms when the cost of the attack is taken into consideration. In addition, we show that on sparse networks, the complexity of this hierarchical power iteration edge removal algorithm is only $O(n\log^{2+\epsilon}(n))$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge