Accelerating Matroid Optimization through Fast Imprecise Oracles

Querying complex models for precise information (e.g. traffic models, database systems, large ML models) often entails intense computations and results in long response times. Thus, weaker models which give imprecise results quickly can be advantageous, provided inaccuracies can be resolved using few queries to a stronger model. In the fundamental problem of computing a maximum-weight basis of a matroid, a well-known generalization of many combinatorial optimization problems, algorithms have access to a clean oracle to query matroid information. We additionally equip algorithms with a fast but dirty oracle modelling an unknown, potentially different matroid. We design and analyze practical algorithms which only use few clean queries w.r.t. the quality of the dirty oracle, while maintaining robustness against arbitrarily poor dirty matroids, approaching the performance of classic algorithms for the given problem. Notably, we prove that our algorithms are, in many respects, best-possible. Further, we outline extensions to other matroid oracle types, non-free dirty oracles and other matroid problems.

Sorting and Hypergraph Orientation under Uncertainty with Predictions

Learning-augmented algorithms have been attracting increasing interest, but have only recently been considered in the setting of explorable uncertainty where precise values of uncertain input elements can be obtained by a query and the goal is to minimize the number of queries needed to solve a problem. We study learning-augmented algorithms for sorting and hypergraph orientation under uncertainty, assuming access to untrusted predictions for the uncertain values. Our algorithms provide improved performance guarantees for accurate predictions while maintaining worst-case guarantees that are best possible without predictions. For hypergraph orientation, for any $\gamma \geq 2$, we give an algorithm that achieves a competitive ratio of $1+1/\gamma$ for correct predictions and $\gamma$ for arbitrarily wrong predictions. For sorting, we achieve an optimal solution for accurate predictions while still being $2$-competitive for arbitrarily wrong predictions. These tradeoffs are the best possible. We also consider different error metrics and show that the performance of our algorithms degrades smoothly with the prediction error in all the cases where this is possible.

Speed-Oblivious Online Scheduling: Knowing (Precise) Speeds is not Necessary

We consider online scheduling on unrelated (heterogeneous) machines in a speed-oblivious setting, where an algorithm is unaware of the exact job-dependent processing speeds. We show strong impossibility results for clairvoyant and non-clairvoyant algorithms and overcome them in models inspired by practical settings: (i) we provide competitive learning-augmented algorithms, assuming that (possibly erroneous) predictions on the speeds are given, and (ii) we provide competitive algorithms for the speed-ordered model, where a single global order of machines according to their unknown job-dependent speeds is known. We prove strong theoretical guarantees and evaluate our findings on a representative heterogeneous multi-core processor. These seem to be the first empirical results for algorithms with predictions that are performed in a non-synthetic environment on real hardware.

Minimalistic Predictions to Schedule Jobs with Online Precedence Constraints

We consider non-clairvoyant scheduling with online precedence constraints, where an algorithm is oblivious to any job dependencies and learns about a job only if all of its predecessors have been completed. Given strong impossibility results in classical competitive analysis, we investigate the problem in a learning-augmented setting, where an algorithm has access to predictions without any quality guarantee. We discuss different prediction models: novel problem-specific models as well as general ones, which have been proposed in previous works. We present lower bounds and algorithmic upper bounds for different precedence topologies, and thereby give a structured overview on which and how additional (possibly erroneous) information helps for designing better algorithms. Along the way, we also improve bounds on traditional competitive ratios for existing algorithms.

A Universal Error Measure for Input Predictions Applied to Online Graph Problems

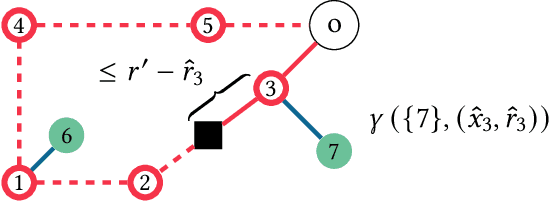
We introduce a novel measure for quantifying the error in input predictions. The error is based on a minimum-cost hyperedge cover in a suitably defined hypergraph and provides a general template which we apply to online graph problems. The measure captures errors due to absent predicted requests as well as unpredicted actual requests; hence, predicted and actual inputs can be of arbitrary size. We achieve refined performance guarantees for previously studied network design problems in the online-list model, such as Steiner tree and facility location. Further, we initiate the study of learning-augmented algorithms for online routing problems, such as the traveling salesperson problem and dial-a-ride problem, where (transportation) requests arrive over time (online-time model). We provide a general algorithmic framework and we give error-dependent performance bounds that improve upon known worst-case barriers, when given accurate predictions, at the cost of slightly increased worst-case bounds when given predictions of arbitrary quality.

Non-Clairvoyant Scheduling with Predictions Revisited

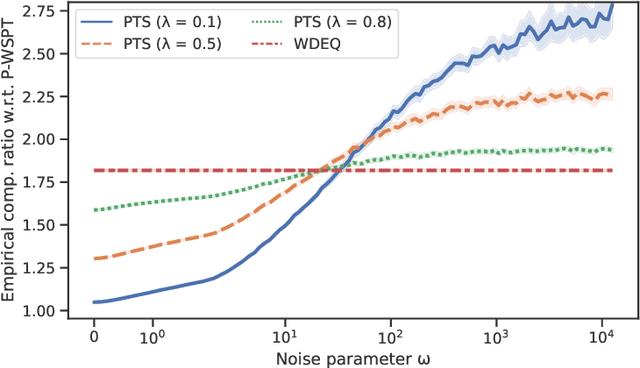
In non-clairvoyant scheduling, the task is to find an online strategy for scheduling jobs with a priori unknown processing requirements with the objective to minimize the total (weighted) completion time. We revisit this well-studied problem in a recently popular learning-augmented setting that integrates (untrusted) predictions in online algorithm design. While previous works used predictions on processing requirements, we propose a new prediction model, which provides a relative order of jobs which could be seen as predicting algorithmic actions rather than parts of the unknown input. We show that these predictions have desired properties, admit a natural error measure as well as algorithms with strong performance guarantees and that they are learnable in both, theory and practice. We generalize the algorithmic framework proposed in the seminal paper by Kumar et al. (NeurIPS'18) and present the first learning-augmented scheduling results for weighted jobs and unrelated machines. We demonstrate in empirical experiments the practicability and superior performance compared to the previously suggested single-machine algorithms.

Robustification of Online Graph Exploration Methods

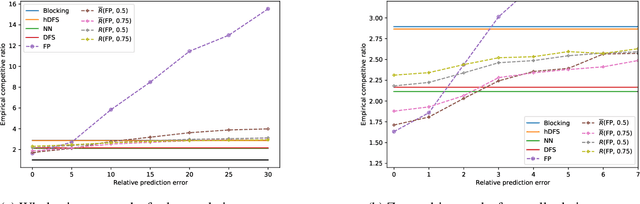
Exploring unknown environments is a fundamental task in many domains, e.g., robot navigation, network security, and internet search. We initiate the study of a learning-augmented variant of the classical, notoriously hard online graph exploration problem by adding access to machine-learned predictions. We propose an algorithm that naturally integrates predictions into the well-known Nearest Neighbor (NN) algorithm and significantly outperforms any known online algorithm if the prediction is of high accuracy while maintaining good guarantees when the prediction is of poor quality. We provide theoretical worst-case bounds that gracefully degrade with the prediction error, and we complement them by computational experiments that confirm our results. Further, we extend our concept to a general framework to robustify algorithms. By interpolating carefully between a given algorithm and NN, we prove new performance bounds that leverage the individual good performance on particular inputs while establishing robustness to arbitrary inputs.

Double Coverage with Machine-Learned Advice

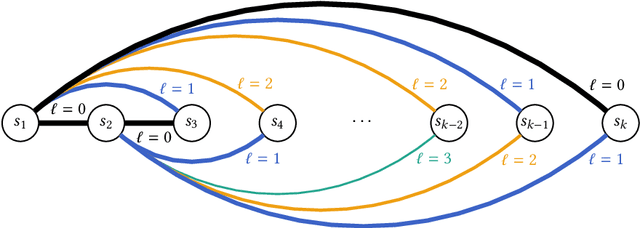
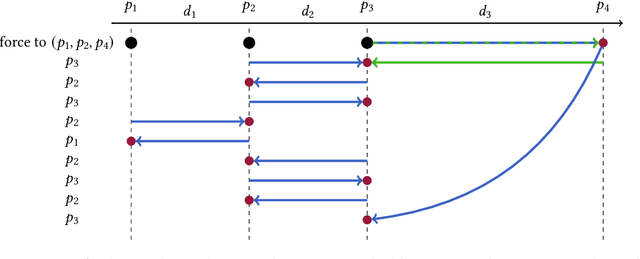
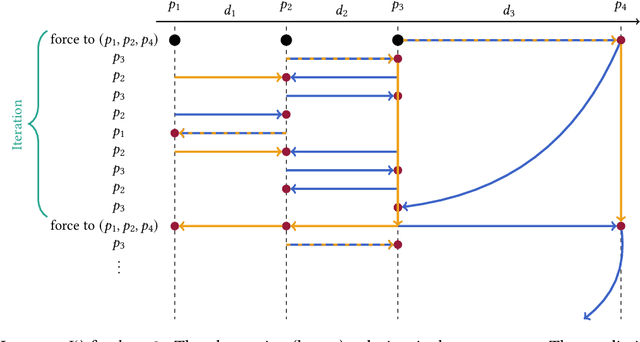
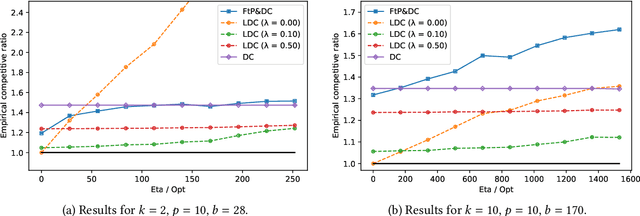
We study the fundamental online $k$-server problem in a learning-augmented setting. While in the traditional online model, an algorithm has no information about the request sequence, we assume that there is given some advice (e.g. machine-learned predictions) on an algorithm's decision. There is, however, no guarantee on the quality of the prediction and it might be far from being correct. Our main result is a learning-augmented variation of the well-known Double Coverage algorithm for k-server on the line (Chrobak et al., SIDMA 1991) in which we integrate predictions as well as our trust into their quality. We give an error-dependent competitive ratio, which is a function of a user-defined trustiness parameter, and which interpolates smoothly between an optimal consistency, the performance in case that all predictions are correct, and the best-possible robustness regardless of the prediction quality. When given good predictions, we improve upon known lower bounds for online algorithms without advice. We further show that our algorithm achieves for any k an almost optimal consistency-robustness tradeoff, within a class of deterministic algorithms respecting local and memoryless properties. Our algorithm outperforms a previously proposed (more general) learning-augmented algorithm. It is remarkable that the previous algorithm heavily exploits memory, whereas our algorithm is memoryless. Finally, we demonstrate in experiments the practicability and the superior performance of our algorithm on real-world data.