Loss Landscape Geometry and the Learning of Symmetries: Or, What Influence Functions Reveal About Robust Generalization

We study how neural emulators of partial differential equation solution operators internalize physical symmetries by introducing an influence-based diagnostic that measures the propagation of parameter updates between symmetry-related states, defined as the metric-weighted overlap of loss gradients evaluated along group orbits. This quantity probes the local geometry of the learned loss landscape and goes beyond forward-pass equivariance tests by directly assessing whether learning dynamics couple physically equivalent configurations. Applying our diagnostic to autoregressive fluid flow emulators, we show that orbit-wise gradient coherence provides the mechanism for learning to generalize over symmetry transformations and indicates when training selects a symmetry compatible basin. The result is a novel technique for evaluating if surrogate models have internalized symmetry properties of the known solution operator.

Why I'm not Answering: Understanding Determinants of Classification of an Abstaining Classifier for Cancer Pathology Reports

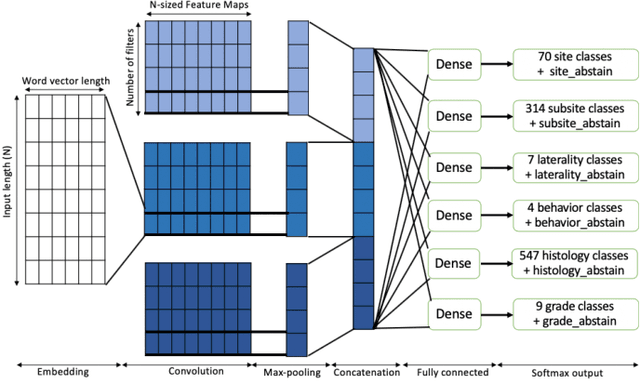
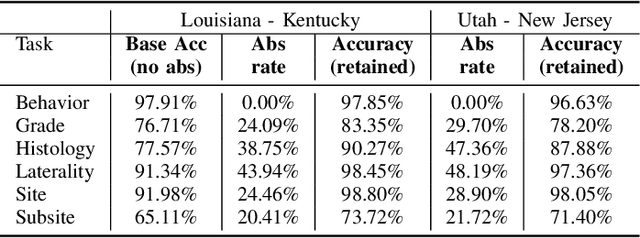
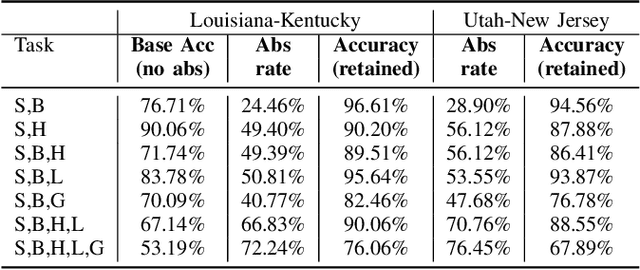
Safe deployment of deep learning systems in critical real world applications requires models to make few mistakes, and only under predictable circumstances. Development of such a model is not yet possible, in general. In this work, we address this problem with an abstaining classifier tuned to have $>$95% accuracy, and identify the determinants of abstention with LIME (the Local Interpretable Model-agnostic Explanations method). Essentially, we are training our model to learn the attributes of pathology reports that are likely to lead to incorrect classifications, albeit at the cost of reduced sensitivity. We demonstrate our method in a multitask setting to classify cancer pathology reports from the NCI SEER cancer registries on six tasks of greatest importance. For these tasks, we reduce the classification error rate by factors of 2-5 by abstaining on 25-45% of the reports. For the specific case of cancer site, we are able to identify metastasis and reports involving lymph nodes as responsible for many of the classification mistakes, and that the extent and types of mistakes vary systematically with cancer site (eg. breast, lung, and prostate). When combining across three of the tasks, our model classifies 50% of the reports with an accuracy greater than 95% for three of the six tasks and greater than 85% for all six tasks on the retained samples. By using this information, we expect to define work flows that incorporate machine learning only in the areas where it is sufficiently robust and accurate, saving human attention to areas where it is required.

Recursive Bias Estimation and $L_2$ Boosting

This paper presents a general iterative bias correction procedure for regression smoothers. This bias reduction schema is shown to correspond operationally to the $L_2$ Boosting algorithm and provides a new statistical interpretation for $L_2$ Boosting. We analyze the behavior of the Boosting algorithm applied to common smoothers $S$ which we show depend on the spectrum of $I-S$. We present examples of common smoother for which Boosting generates a divergent sequence. The statistical interpretation suggest combining algorithm with an appropriate stopping rule for the iterative procedure. Finally we illustrate the practical finite sample performances of the iterative smoother via a simulation study. simulations.