Cartan moving frames and the data manifolds

The purpose of this paper is to employ the language of Cartan moving frames to study the geometry of the data manifolds and its Riemannian structure, via the data information metric and its curvature at data points. Using this framework and through experiments, explanations on the response of a neural network are given by pointing out the output classes that are easily reachable from a given input. This emphasizes how the proposed mathematical relationship between the output of the network and the geometry of its inputs can be exploited as an explainable artificial intelligence tool.

MIQCQP reformulation of the ReLU neural networks Lipschitz constant estimation problem

It is well established that to ensure or certify the robustness of a neural network, its Lipschitz constant plays a prominent role. However, its calculation is NP-hard. In this note, by taking into account activation regions at each layer as new constraints, we propose new quadratically constrained MIP formulations for the neural network Lipschitz estimation problem. The solutions of these problems give lower bounds and upper bounds of the Lipschitz constant and we detail conditions when they coincide with the exact Lipschitz constant.

Canonical foliations of neural networks: application to robustness

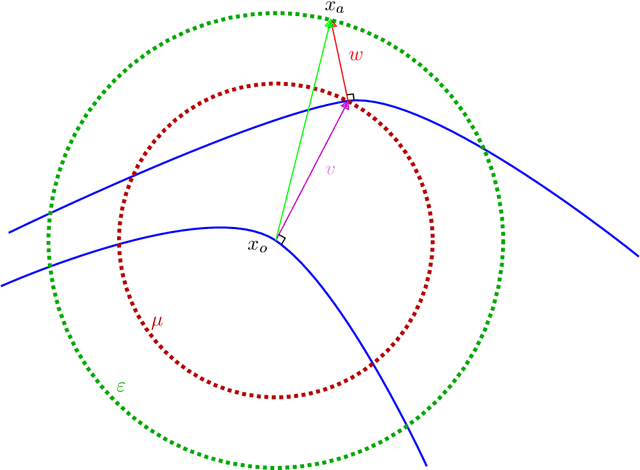
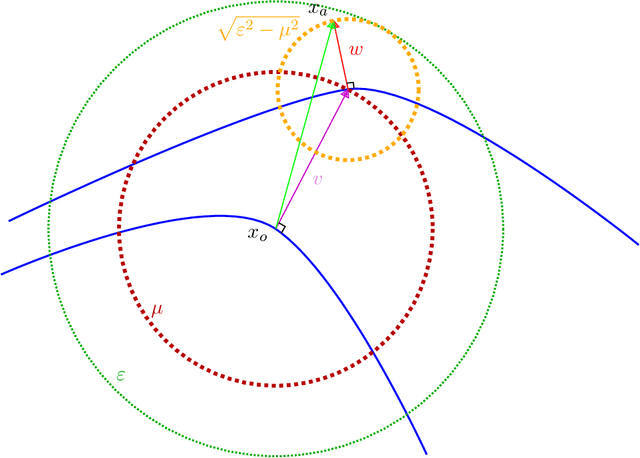
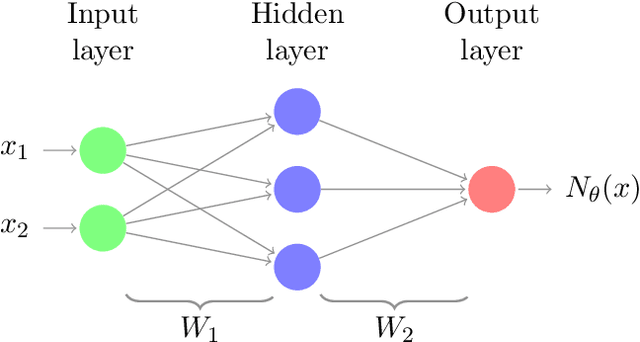
Adversarial attack is an emerging threat to the trustability of machine learning. Understanding these attacks is becoming a crucial task. We propose a new vision on neural network robustness using Riemannian geometry and foliation theory, and create a new adversarial attack by taking into account the curvature of the data space. This new adversarial attack called the "dog-leg attack" is a two-step approximation of a geodesic in the data space. The data space is treated as a (pseudo) Riemannian manifold equipped with the pullback of the Fisher Information Metric (FIM) of the neural network. In most cases, this metric is only semi-definite and its kernel becomes a central object to study. A canonical foliation is derived from this kernel. The curvature of the foliation's leaves gives the appropriate correction to get a two-step approximation of the geodesic and hence a new efficient adversarial attack. Our attack is tested on a toy example, a neural network trained to mimic the $\texttt{Xor}$ function, and demonstrates better results that the state of the art attack presented by Zhao et al. (2019).

Robust SVM Optimization in Banach spaces

We address the issue of binary classification in Banach spaces in presence of uncertainty. We show that a number of results from classical support vector machines theory can be appropriately generalised to their robust counterpart in Banach spaces. These include the Representer Theorem, strong duality for the associated Optimization problem as well as their geometric interpretation. Furthermore, we propose a game theoretic interpretation by expressing a Nash equilibrium problem formulation for the more general problem of finding the closest points in two closed convex sets when the underlying space is reflexive and smooth.

Convolutional Neural Network for Multipath Detection in GNSS Receivers

Global Navigation Satellite System (GNSS) signals are subject to different kinds of events causing significant errors in positioning. This work explores the application of Machine Learning (ML) methods of anomaly detection applied to GNSS receiver signals. More specifically, our study focuses on multipath contamination, using samples of the correlator output signal. The GPS L1 C/A signal data is used and sourced directly from the correlator output. To extract the important features and patterns from such data, we use deep convolutional neural networks (CNN), which have proven to be efficient in image analysis in particular. To take advantage of CNN, the correlator output signal is mapped as a 2D input image and fed to the convolutional layers of a neural network. The network automatically extracts the relevant features from the input samples and proceeds with the multipath detection. We train the CNN using synthetic signals. To optimize the model architecture with respect to the GNSS correlator complexity, the evaluation of the CNN performance is done as a function of the number of correlator output points.

Using Wasserstein-2 regularization to ensure fair decisions with Neural-Network classifiers

In this paper, we propose a new method to build fair Neural-Network classifiers by using a constraint based on the Wasserstein distance. More specifically, we detail how to efficiently compute the gradients of Wasserstein-2 regularizers for Neural-Networks. The proposed strategy is then used to train Neural-Networks decision rules which favor fair predictions. Our method fully takes into account two specificities of Neural-Networks training: (1) The network parameters are indirectly learned based on automatic differentiation and on the loss gradients, and (2) batch training is the gold standard to approximate the parameter gradients, as it requires a reasonable amount of computations and it can efficiently explore the parameters space. Results are shown on synthetic data, as well as on the UCI Adult Income Dataset. Our method is shown to perform well compared with 'ZafarICWWW17' and linear-regression with Wasserstein-1 regularization, as in 'JiangUAI19', in particular when non-linear decision rules are required for accurate predictions.

The coupling effect of Lipschitz regularization in deep neural networks

We investigate robustness of deep feed-forward neural networks when input data are subject to random uncertainties. More specifically, we consider regularization of the network by its Lipschitz constant and emphasize its role. We highlight the fact that this regularization is not only a way to control the magnitude of the weights but has also a coupling effect on the network weights accross the layers. We claim and show evidence on a dataset that this coupling effect brings a tradeoff between robustness and expressiveness of the network. This suggests that Lipschitz regularization should be carefully implemented so as to maintain coupling accross layers.

Feature uncertainty bounding schemes for large robust nonlinear SVM classifiers

We consider the binary classification problem when data are large and subject to unknown but bounded uncertainties. We address the problem by formulating the nonlinear support vector machine training problem with robust optimization. To do so, we analyze and propose two bounding schemes for uncertainties associated to random approximate features in low dimensional spaces. The proposed techniques are based on Random Fourier Features and the Nystr\"om methods. The resulting formulations can be solved with efficient stochastic approximation techniques such as stochastic (sub)-gradient, stochastic proximal gradient techniques or their variants.