Cartan moving frames and the data manifolds

The purpose of this paper is to employ the language of Cartan moving frames to study the geometry of the data manifolds and its Riemannian structure, via the data information metric and its curvature at data points. Using this framework and through experiments, explanations on the response of a neural network are given by pointing out the output classes that are easily reachable from a given input. This emphasizes how the proposed mathematical relationship between the output of the network and the geometry of its inputs can be exploited as an explainable artificial intelligence tool.

Canonical foliations of neural networks: application to robustness

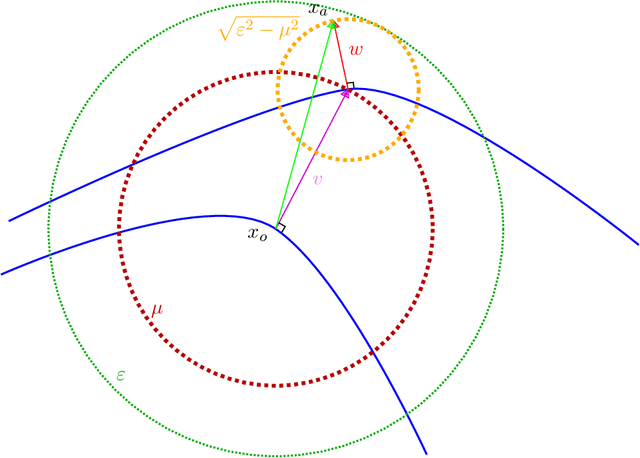
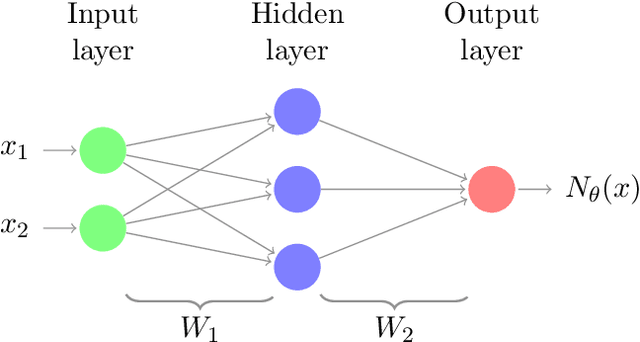
Adversarial attack is an emerging threat to the trustability of machine learning. Understanding these attacks is becoming a crucial task. We propose a new vision on neural network robustness using Riemannian geometry and foliation theory, and create a new adversarial attack by taking into account the curvature of the data space. This new adversarial attack called the "dog-leg attack" is a two-step approximation of a geodesic in the data space. The data space is treated as a (pseudo) Riemannian manifold equipped with the pullback of the Fisher Information Metric (FIM) of the neural network. In most cases, this metric is only semi-definite and its kernel becomes a central object to study. A canonical foliation is derived from this kernel. The curvature of the foliation's leaves gives the appropriate correction to get a two-step approximation of the geodesic and hence a new efficient adversarial attack. Our attack is tested on a toy example, a neural network trained to mimic the $\texttt{Xor}$ function, and demonstrates better results that the state of the art attack presented by Zhao et al. (2019).