Proving Conjectures Acquired by Composing Multiple Biases

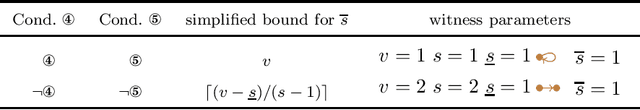
We present the proofs of the conjectures mentioned in the paper published in the proceedings of the 2024 AAAI conference [1], and discovered by the decomposition methods presented in the same paper.

Classifying Pattern and Feature Properties to Get a $Θ(n)$ Checker and Reformulation for Sliding Time-Series Constraints

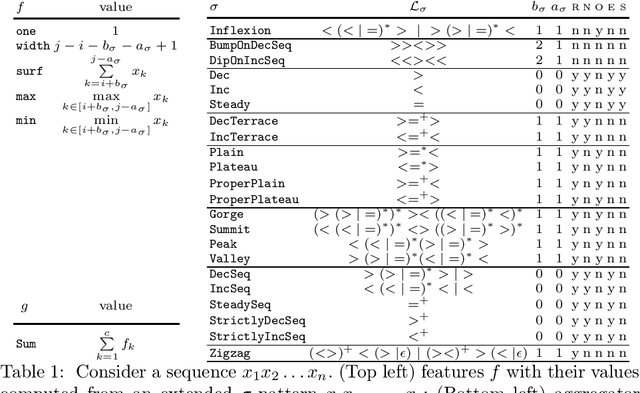
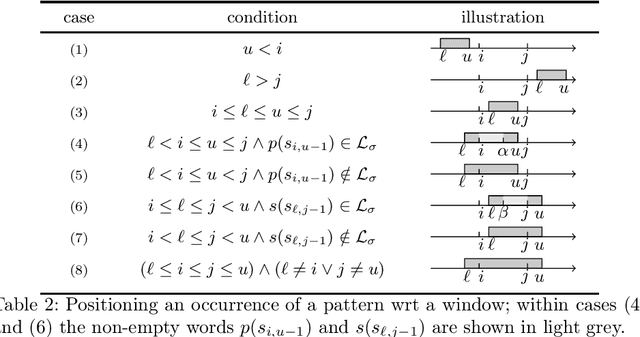
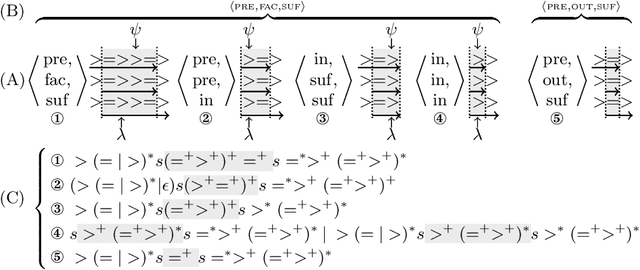
Given, a sequence $\mathcal{X}$ of $n$ variables, a time-series constraint ctr using the Sum aggregator, and a sliding time-series constraint enforcing the constraint ctr on each sliding window of $\mathcal{X}$ of $m$ consecutive variables, we describe a $\Theta(n)$ time complexity checker, as well as a $\Theta(n)$ space complexity reformulation for such sliding constraint.

Synthesising a Database of Parameterised Linear and Non-Linear Invariants for Time-Series Constraints

Many constraints restricting the result of some computations over an integer sequence can be compactly represented by register automata. We improve the propagation of the conjunction of such constraints on the same sequence by synthesising a database of linear and non-linear invariants using their register-automaton representation. The obtained invariants are formulae parameterised by a function of the sequence length and proven to be true for any long enough sequence. To assess the quality of such linear invariants, we developed a method to verify whether a generated linear invariant is a facet of the convex hull of the feasible points. This method, as well as the proof of non-linear invariants, are based on the systematic generation of constant-size deterministic finite automata that accept all integer sequences whose result verifies some simple condition. We apply such methodology to a set of 44 time-series constraints and obtain 1400 linear invariants from which 70% are facet defining, and 600 non-linear invariants, which were tested on short-term electricity production problems.

Global Constraint Catalog, Volume II, Time-Series Constraints

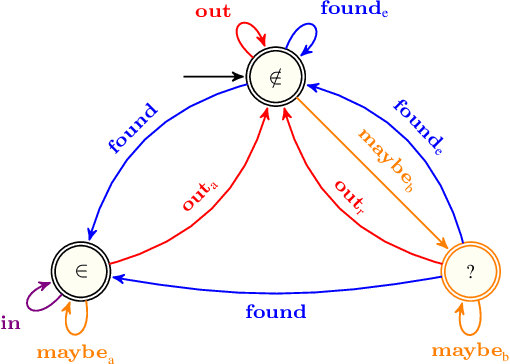
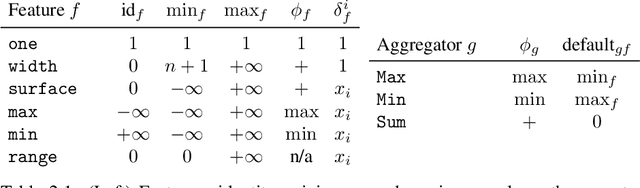
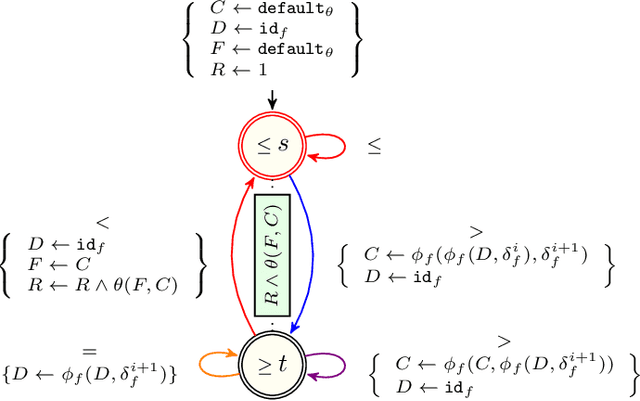
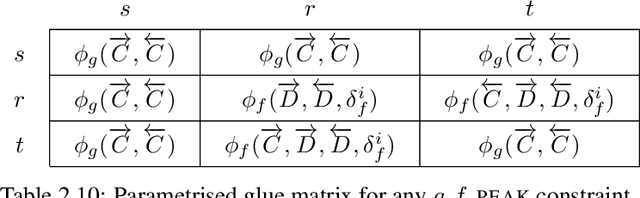
First this report presents a restricted set of finite transducers used to synthesise structural time-series constraints described by means of a multi-layered function composition scheme. Second it provides the corresponding synthesised catalogue of structural time-series constraints where each constraint is explicitly described in terms of automata with registers.

Propagating Regular Counting Constraints

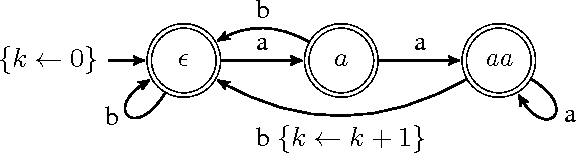
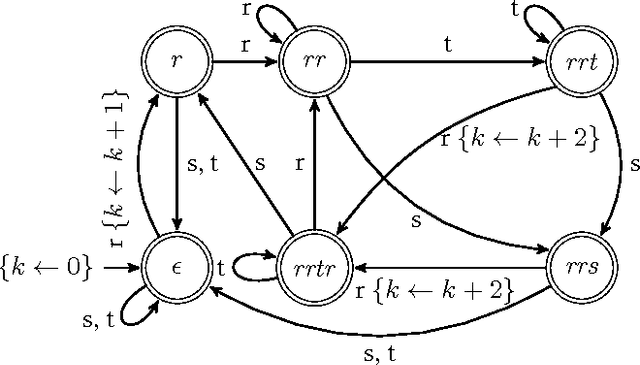
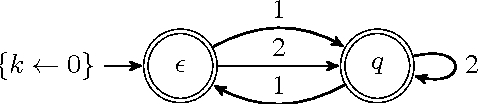
Constraints over finite sequences of variables are ubiquitous in sequencing and timetabling. Moreover, the wide variety of such constraints in practical applications led to general modelling techniques and generic propagation algorithms, often based on deterministic finite automata (DFA) and their extensions. We consider counter-DFAs (cDFA), which provide concise models for regular counting constraints, that is constraints over the number of times a regular-language pattern occurs in a sequence. We show how to enforce domain consistency in polynomial time for atmost and atleast regular counting constraints based on the frequent case of a cDFA with only accepting states and a single counter that can be incremented by transitions. We also prove that the satisfaction of exact regular counting constraints is NP-hard and indicate that an incomplete algorithm for exact regular counting constraints is faster and provides more pruning than the existing propagator from [3]. Regular counting constraints are closely related to the CostRegular constraint but contribute both a natural abstraction and some computational advantages.

A Generalized Arc-Consistency Algorithm for a Class of Counting Constraints: Revised Edition that Incorporates One Correction

This paper introduces the SEQ BIN meta-constraint with a polytime algorithm achieving general- ized arc-consistency according to some properties. SEQ BIN can be used for encoding counting con- straints such as CHANGE, SMOOTH or INCREAS- ING NVALUE. For some of these constraints and some of their variants GAC can be enforced with a time and space complexity linear in the sum of domain sizes, which improves or equals the best known results of the literature.