Propagating Regular Counting Constraints
Paper and Code
Sep 27, 2013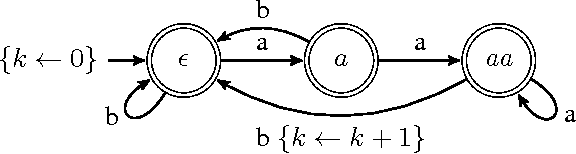

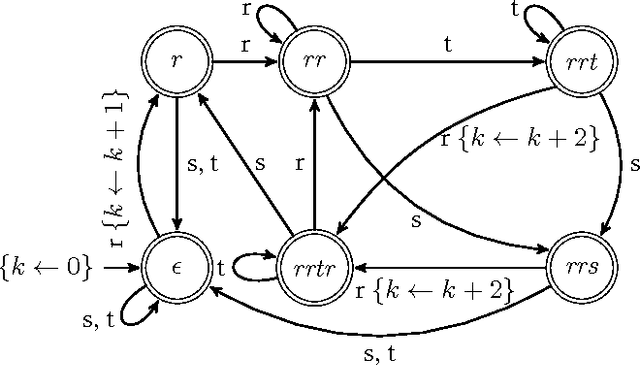
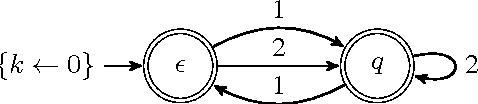
Constraints over finite sequences of variables are ubiquitous in sequencing and timetabling. Moreover, the wide variety of such constraints in practical applications led to general modelling techniques and generic propagation algorithms, often based on deterministic finite automata (DFA) and their extensions. We consider counter-DFAs (cDFA), which provide concise models for regular counting constraints, that is constraints over the number of times a regular-language pattern occurs in a sequence. We show how to enforce domain consistency in polynomial time for atmost and atleast regular counting constraints based on the frequent case of a cDFA with only accepting states and a single counter that can be incremented by transitions. We also prove that the satisfaction of exact regular counting constraints is NP-hard and indicate that an incomplete algorithm for exact regular counting constraints is faster and provides more pruning than the existing propagator from [3]. Regular counting constraints are closely related to the CostRegular constraint but contribute both a natural abstraction and some computational advantages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge