Hyperspectral-Multispectral Image Fusion with Weighted LASSO

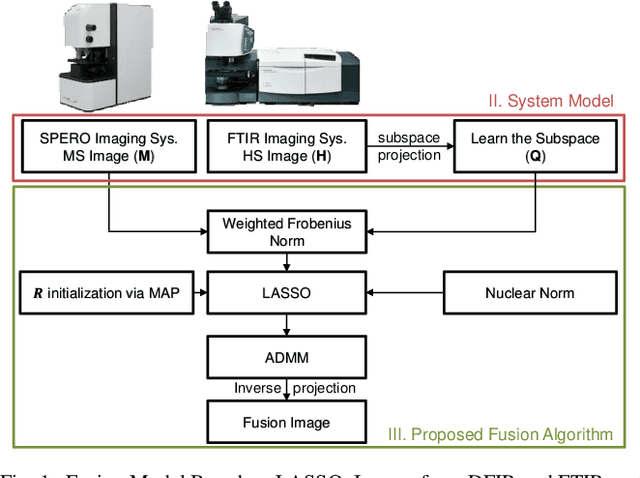
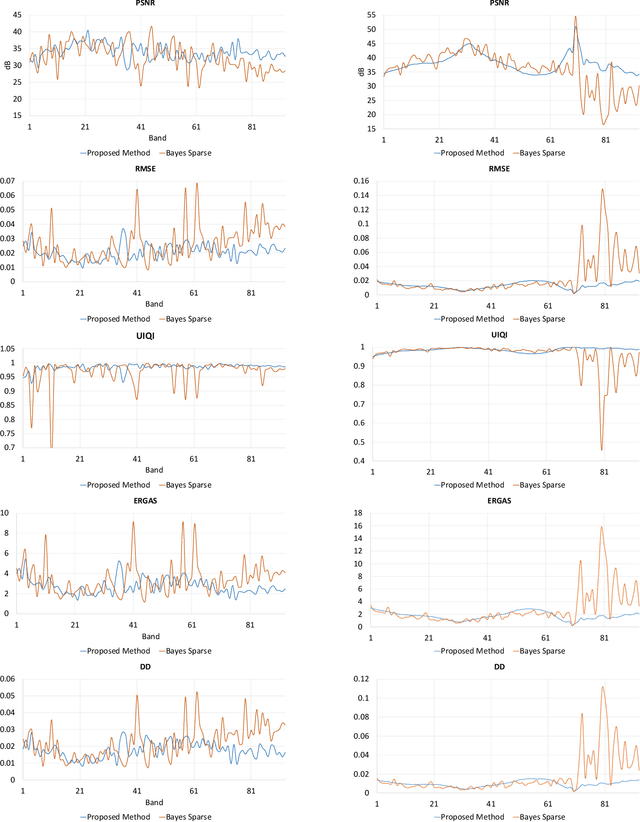
Spectral imaging enables spatially-resolved identification of materials in remote sensing, biomedicine, and astronomy. However, acquisition times require balancing spectral and spatial resolution with signal-to-noise. Hyperspectral imaging provides superior material specificity, while multispectral images are faster to collect at greater fidelity. We propose an approach for fusing hyperspectral and multispectral images to provide high-quality hyperspectral output. The proposed optimization leverages the least absolute shrinkage and selection operator (LASSO) to perform variable selection and regularization. Computational time is reduced by applying the alternating direction method of multipliers (ADMM), as well as initializing the fusion image by estimating it using maximum a posteriori (MAP) based on Hardie's method. We demonstrate that the proposed sparse fusion and reconstruction provides quantitatively superior results when compared to existing methods on publicly available images. Finally, we show how the proposed method can be practically applied in biomedical infrared spectroscopic microscopy.

Localized Linear Regression in Networked Data

The network Lasso (nLasso) has been proposed recently as an efficient learning algorithm for massive networked data sets (big data over networks). It extends the well-known least least absolute shrinkage and selection operator (Lasso) from learning sparse (generalized) linear models to network models. Efficient implementations of the nLasso have been obtained using convex optimization methods. These implementations naturally lend to highly scalable message passing methods. In this paper, we analyze the performance of nLasso when applied to localized linear regression problems involving networked data. Our main result is a sufficient conditions on the network structure and available label information such that nLasso accurately learns a localized linear regression model from few labeled data points.

Classifying Partially Labeled Networked Data via Logistic Network Lasso

We apply the network Lasso to classify partially labeled data points which are characterized by high-dimensional feature vectors. In order to learn an accurate classifier from limited amounts of labeled data, we borrow statistical strength, via an intrinsic network structure, across the dataset. The resulting logistic network Lasso amounts to a regularized empirical risk minimization problem using the total variation of a classifier as a regularizer. This minimization problem is a non-smooth convex optimization problem which we solve using a primal-dual splitting method. This method is appealing for big data applications as it can be implemented as a highly scalable message passing algorithm.

The Logistic Network Lasso

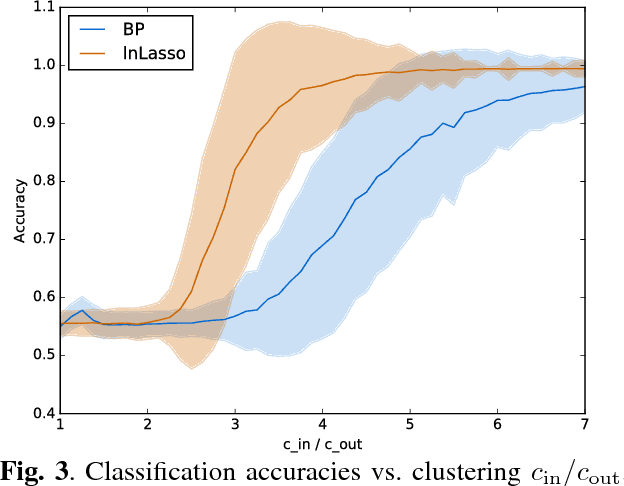
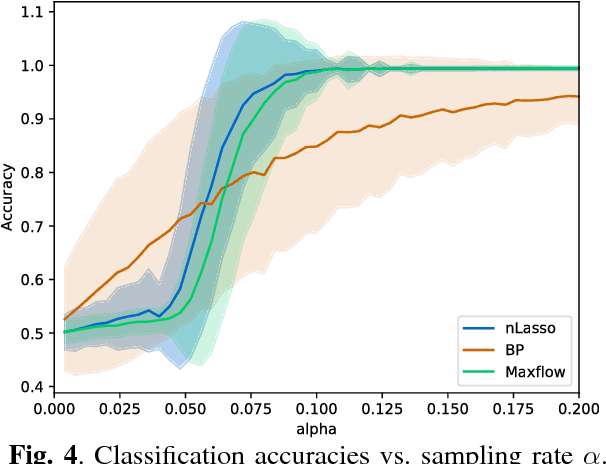
We apply the network Lasso to solve binary classification and clustering problems for network-structured data. To this end, we generalize ordinary logistic regression to non-Euclidean data with an intrinsic network structure. The resulting "logistic network Lasso" amounts to solving a non-smooth convex regularized empirical risk minimization. The risk is measured using the logistic loss incurred over a small set of labeled nodes. For the regularization, we propose to use the total variation of the classifier requiring it to conform to the underlying network structure. A scalable implementation of the learning method is obtained using an inexact variant of the alternating direction methods of multipliers which results in a scalable learning algorithm

When is Network Lasso Accurate: The Vector Case

A recently proposed learning algorithm for massive network-structured data sets (big data over networks) is the network Lasso (nLasso), which extends the well- known Lasso estimator from sparse models to network-structured datasets. Efficient implementations of the nLasso have been presented using modern convex optimization methods. In this paper, we provide sufficient conditions on the network structure and available label information such that nLasso accurately learns a vector-valued graph signal (representing label information) from the information provided by the labels of a few data points.