The Logistic Network Lasso
Paper and Code
Aug 14, 2018

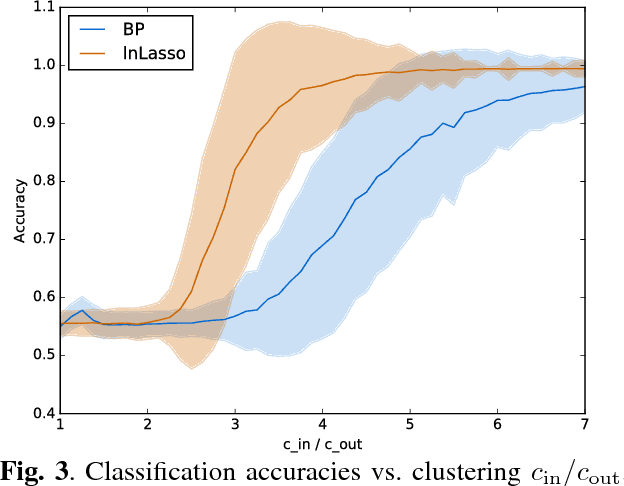
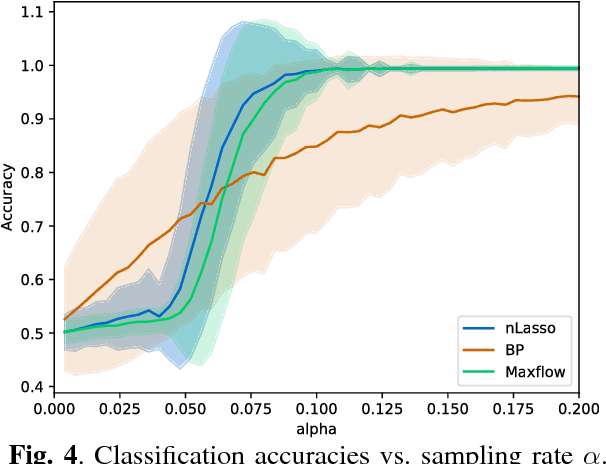
We apply the network Lasso to solve binary classification and clustering problems for network-structured data. To this end, we generalize ordinary logistic regression to non-Euclidean data with an intrinsic network structure. The resulting "logistic network Lasso" amounts to solving a non-smooth convex regularized empirical risk minimization. The risk is measured using the logistic loss incurred over a small set of labeled nodes. For the regularization, we propose to use the total variation of the classifier requiring it to conform to the underlying network structure. A scalable implementation of the learning method is obtained using an inexact variant of the alternating direction methods of multipliers which results in a scalable learning algorithm
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge