Classifying Partially Labeled Networked Data via Logistic Network Lasso

We apply the network Lasso to classify partially labeled data points which are characterized by high-dimensional feature vectors. In order to learn an accurate classifier from limited amounts of labeled data, we borrow statistical strength, via an intrinsic network structure, across the dataset. The resulting logistic network Lasso amounts to a regularized empirical risk minimization problem using the total variation of a classifier as a regularizer. This minimization problem is a non-smooth convex optimization problem which we solve using a primal-dual splitting method. This method is appealing for big data applications as it can be implemented as a highly scalable message passing algorithm.

The Logistic Network Lasso

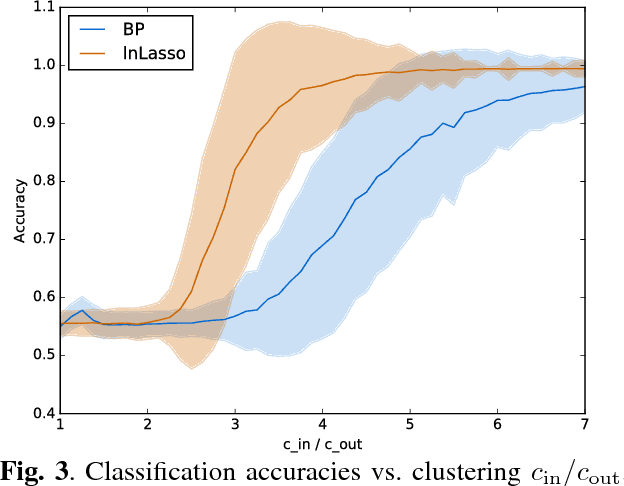
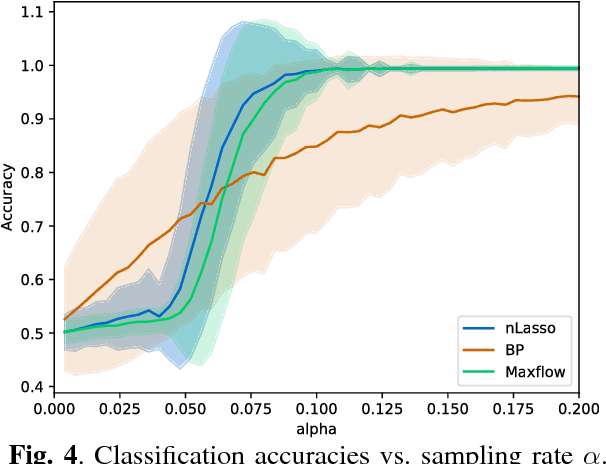
We apply the network Lasso to solve binary classification and clustering problems for network-structured data. To this end, we generalize ordinary logistic regression to non-Euclidean data with an intrinsic network structure. The resulting "logistic network Lasso" amounts to solving a non-smooth convex regularized empirical risk minimization. The risk is measured using the logistic loss incurred over a small set of labeled nodes. For the regularization, we propose to use the total variation of the classifier requiring it to conform to the underlying network structure. A scalable implementation of the learning method is obtained using an inexact variant of the alternating direction methods of multipliers which results in a scalable learning algorithm