Prediction and compression of lattice QCD data using machine learning algorithms on quantum annealer

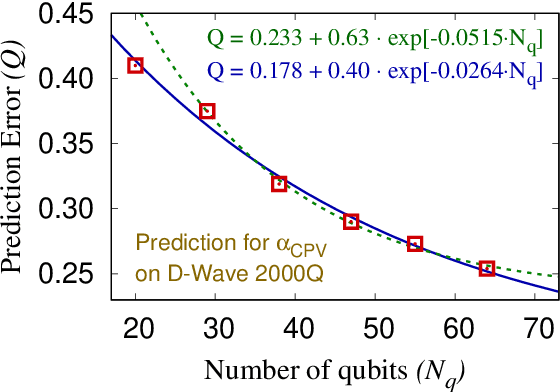
We present regression and compression algorithms for lattice QCD data utilizing the efficient binary optimization ability of quantum annealers. In the regression algorithm, we encode the correlation between the input and output variables into a sparse coding machine learning algorithm. The trained correlation pattern is used to predict lattice QCD observables of unseen lattice configurations from other observables measured on the lattice. In the compression algorithm, we define a mapping from lattice QCD data of floating-point numbers to the binary coefficients that closely reconstruct the input data from a set of basis vectors. Since the reconstruction is not exact, the mapping defines a lossy compression, but, a reasonably small number of binary coefficients are able to reconstruct the input vector of lattice QCD data with the reconstruction error much smaller than the statistical fluctuation. In both applications, we use D-Wave quantum annealers to solve the NP-hard binary optimization problems of the machine learning algorithms.

Lossy compression of statistical data using quantum annealer

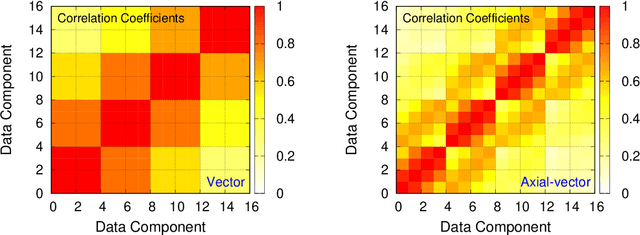
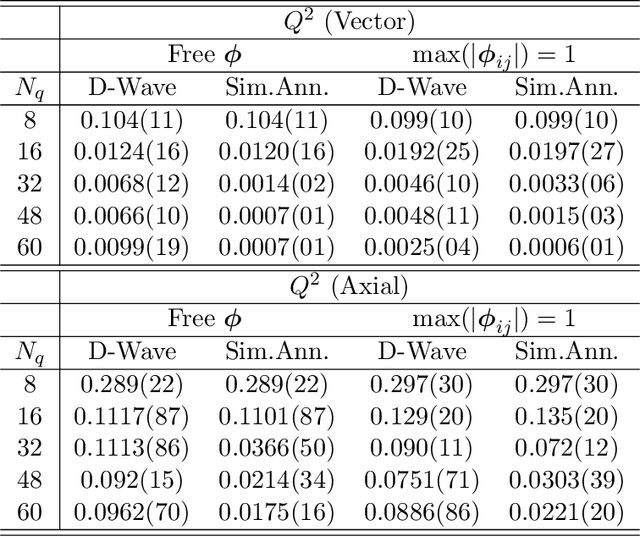
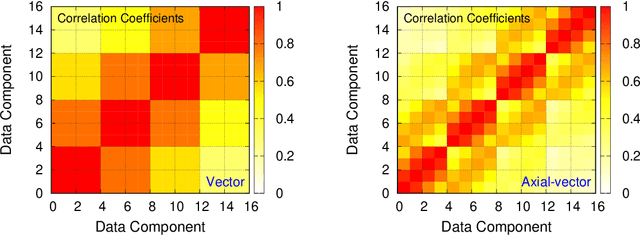
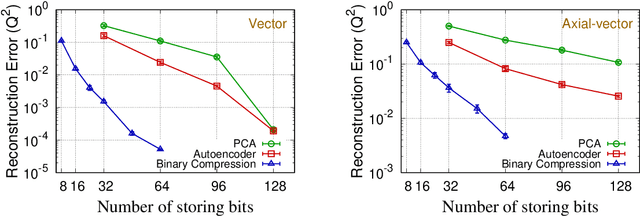
We present a new lossy compression algorithm for statistical floating-point data through a representation learning with binary variables. The algorithm finds a set of basis vectors and their binary coefficients that precisely reconstruct the original data. The optimization for the basis vectors is performed classically, while binary coefficients are retrieved through both simulated and quantum annealing for comparison. A bias correction procedure is also presented to estimate and eliminate the error and bias introduced from the inexact reconstruction of the lossy compression for statistical data analyses. The compression algorithm is demonstrated on two different datasets of lattice quantum chromodynamics simulations. The results obtained using simulated annealing show 3.5 times better compression performance than the algorithms based on a neural-network autoencoder and principal component analysis. Calculations using quantum annealing also show promising results, but performance is limited by the integrated control error of the quantum processing unit, which yields large uncertainties in the biases and coupling parameters. Hardware comparison is further studied between the previous generation D-Wave 2000Q and the current D-Wave Advantage system. Our study shows that the Advantage system is more likely to obtain low-energy solutions for the problems than the 2000Q.

A regression algorithm for accelerated lattice QCD that exploits sparse inference on the D-Wave quantum annealer

We propose a regression algorithm that utilizes a learned dictionary optimized for sparse inference on D-Wave quantum annealer. In this regression algorithm, we concatenate the independent and dependent variables as an combined vector, and encode the high-order correlations between them into a dictionary optimized for sparse reconstruction. On a test dataset, the dependent variable is initialized to its average value and then a sparse reconstruction of the combined vector is obtained in which the dependent variable is typically shifted closer to its true value, as in a standard inpainting or denoising task. Here, a quantum annealer, which can presumably exploit a fully entangled initial state to better explore the complex energy landscape, is used to solve the highly non-convex sparse coding optimization problem. The regression algorithm is demonstrated for a lattice quantum chromodynamics simulation data using a D-Wave 2000Q quantum annealer and good prediction performance is achieved. The regression test is performed using six different values for the number of fully connected logical qubits, between 20 and 64, the latter being the maximum that can be embedded on the D-Wave 2000Q. The scaling results indicate that a larger number of qubits gives better prediction accuracy, the best performance being comparable to the best classical regression algorithms reported so far.

Image classification using quantum inference on the D-Wave 2X

We use a quantum annealing D-Wave 2X computer to obtain solutions to NP-hard sparse coding problems. To reduce the dimensionality of the sparse coding problem to fit on the quantum D-Wave 2X hardware, we passed downsampled MNIST images through a bottleneck autoencoder. To establish a benchmark for classification performance on this reduced dimensional data set, we used an AlexNet-like architecture implemented in TensorFlow, obtaining a classification score of $94.54 \pm 0.7 \%$. As a control, we showed that the same AlexNet-like architecture produced near-state-of-the-art classification performance $(\sim 99\%)$ on the original MNIST images. To obtain a set of optimized features for inferring sparse representations of the reduced dimensional MNIST dataset, we imprinted on a random set of $47$ image patches followed by an off-line unsupervised learning algorithm using stochastic gradient descent to optimize for sparse coding. Our single-layer of sparse coding matched the stride and patch size of the first convolutional layer of the AlexNet-like deep neural network and contained $47$ fully-connected features, $47$ being the maximum number of dictionary elements that could be embedded onto the D-Wave $2$X hardware. Recent work suggests that the optimal level of sparsity corresponds to a critical value of the trade-off parameter associated with a putative second order phase transition, an observation supported by a free energy analysis of D-Wave energy states. When the sparse representations inferred by the D-Wave $2$X were passed to a linear support vector machine, we obtained a classification score of $95.68\%$. Thus, on this problem, we find that a single-layer of quantum inference is able to outperform a standard deep neural network architecture.