Prediction and compression of lattice QCD data using machine learning algorithms on quantum annealer

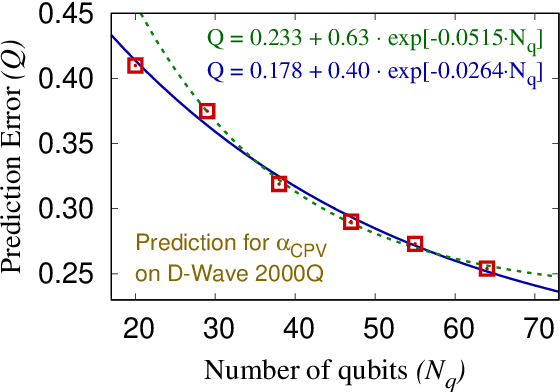
We present regression and compression algorithms for lattice QCD data utilizing the efficient binary optimization ability of quantum annealers. In the regression algorithm, we encode the correlation between the input and output variables into a sparse coding machine learning algorithm. The trained correlation pattern is used to predict lattice QCD observables of unseen lattice configurations from other observables measured on the lattice. In the compression algorithm, we define a mapping from lattice QCD data of floating-point numbers to the binary coefficients that closely reconstruct the input data from a set of basis vectors. Since the reconstruction is not exact, the mapping defines a lossy compression, but, a reasonably small number of binary coefficients are able to reconstruct the input vector of lattice QCD data with the reconstruction error much smaller than the statistical fluctuation. In both applications, we use D-Wave quantum annealers to solve the NP-hard binary optimization problems of the machine learning algorithms.

Lossy compression of statistical data using quantum annealer

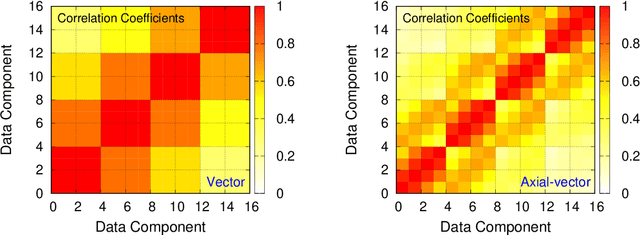
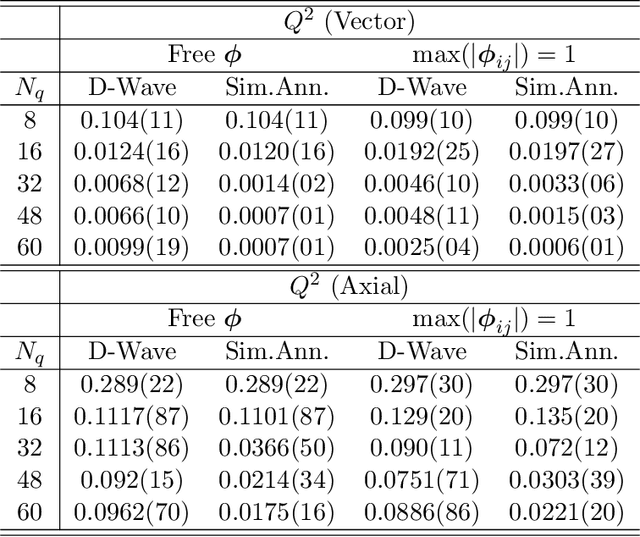
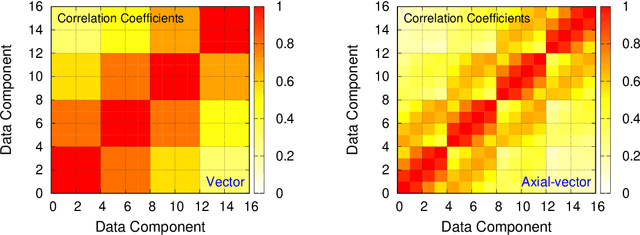
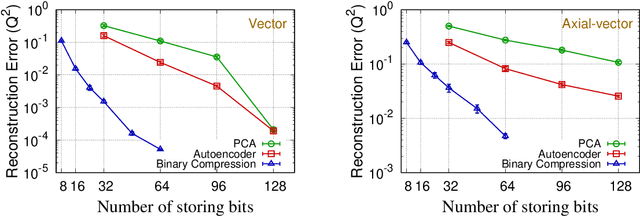
We present a new lossy compression algorithm for statistical floating-point data through a representation learning with binary variables. The algorithm finds a set of basis vectors and their binary coefficients that precisely reconstruct the original data. The optimization for the basis vectors is performed classically, while binary coefficients are retrieved through both simulated and quantum annealing for comparison. A bias correction procedure is also presented to estimate and eliminate the error and bias introduced from the inexact reconstruction of the lossy compression for statistical data analyses. The compression algorithm is demonstrated on two different datasets of lattice quantum chromodynamics simulations. The results obtained using simulated annealing show 3.5 times better compression performance than the algorithms based on a neural-network autoencoder and principal component analysis. Calculations using quantum annealing also show promising results, but performance is limited by the integrated control error of the quantum processing unit, which yields large uncertainties in the biases and coupling parameters. Hardware comparison is further studied between the previous generation D-Wave 2000Q and the current D-Wave Advantage system. Our study shows that the Advantage system is more likely to obtain low-energy solutions for the problems than the 2000Q.

A machine learning approach for efficient multi-dimensional integration

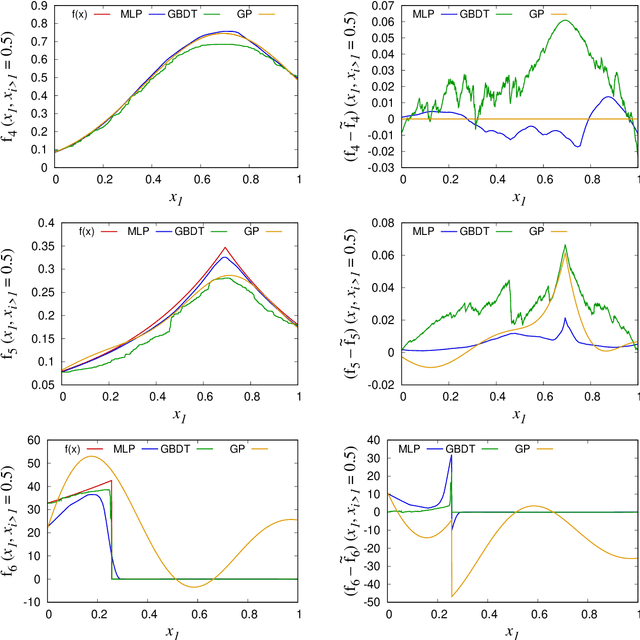
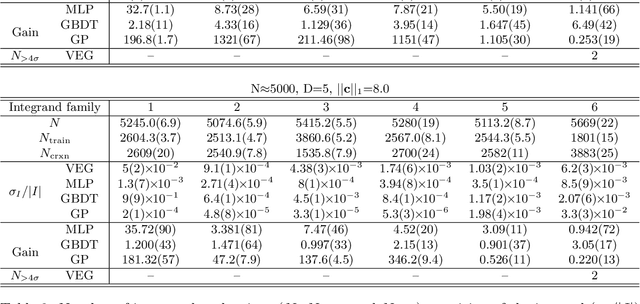
We propose a novel multi-dimensional integration algorithm using a machine learning (ML) technique. After training a ML regression model to mimic a target integrand, the regression model is used to evaluate an approximation of the integral. Then, the difference between the approximation and the true answer is calculated to correct the bias in the approximation of the integral induced by a ML prediction error. Because of the bias correction, the final estimate of the integral is unbiased and has a statistically correct error estimation. The performance of the proposed algorithm is demonstrated on six different types of integrands at various dimensions and integrand difficulties. The results show that, for the same total number of integrand evaluations, the new algorithm provides integral estimates with more than an order of magnitude smaller uncertainties than those of the VEGAS algorithm in most of the test cases.

A regression algorithm for accelerated lattice QCD that exploits sparse inference on the D-Wave quantum annealer

We propose a regression algorithm that utilizes a learned dictionary optimized for sparse inference on D-Wave quantum annealer. In this regression algorithm, we concatenate the independent and dependent variables as an combined vector, and encode the high-order correlations between them into a dictionary optimized for sparse reconstruction. On a test dataset, the dependent variable is initialized to its average value and then a sparse reconstruction of the combined vector is obtained in which the dependent variable is typically shifted closer to its true value, as in a standard inpainting or denoising task. Here, a quantum annealer, which can presumably exploit a fully entangled initial state to better explore the complex energy landscape, is used to solve the highly non-convex sparse coding optimization problem. The regression algorithm is demonstrated for a lattice quantum chromodynamics simulation data using a D-Wave 2000Q quantum annealer and good prediction performance is achieved. The regression test is performed using six different values for the number of fully connected logical qubits, between 20 and 64, the latter being the maximum that can be embedded on the D-Wave 2000Q. The scaling results indicate that a larger number of qubits gives better prediction accuracy, the best performance being comparable to the best classical regression algorithms reported so far.

Estimation of matrix trace using machine learning

We present a new trace estimator of the matrix whose explicit form is not given but its matrix multiplication to a vector is available. The form of the estimator is similar to the Hutchison stochastic trace estimator, but instead of the random noise vectors in Hutchison estimator, we use small number of probing vectors determined by machine learning. Evaluation of the quality of estimates and bias correction are discussed. An unbiased estimator is proposed for the calculation of the expectation value of a function of traces. In the numerical experiments with random matrices, it is shown that the precision of trace estimates with $\mathcal{O}(10)$ probing vectors determined by the machine learning is similar to that with $\mathcal{O}(10000)$ random noise vectors.